题目内容
5.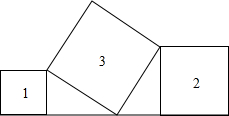 已知正方形①、②在直线上,正方形③如图放置,若正方形①、②的面积分别81cm2和144cm2,则正方形③的边长为( )
已知正方形①、②在直线上,正方形③如图放置,若正方形①、②的面积分别81cm2和144cm2,则正方形③的边长为( )| A. | 225 | B. | 63 | C. | 50 | D. | 15 |
分析 根据正方形的性质就可以得出∠EAB=∠EBD=∠BCD=90°,BE=BD,∠AEB=∠CBD,就可以得出△ABE≌△CDB,得出AE=BC,AB=CD,由勾股定理就可以得出BE的值,进而得出结论.
解答  解:∵四边形①、②、③都是正方形,
解:∵四边形①、②、③都是正方形,
∴∠EAB=∠EBD=∠BCD=90°,BE=BD,
∴∠AEB+∠ABE=90°,∠ABE+∠DBC=90°,
∴∠AEB=∠CBD.
在△ABE和△CDB中,
$\left\{\begin{array}{l}∠EAB=∠BCD\\∠AEB=∠CBD\\ BE=DB\end{array}\right.$,
∴△ABE≌△CDB(AAS),
∴AE=BC,AB=CD.
∵正方形①、②的面积分别81cm2和144cm2,
∴AE2=81,CD2=144.
∴AB2=63.
在Rt△ABE中,由勾股定理,得
BE2=AE2+AB2=81+144=225,
∴BE=15.
故选D.
点评 本题考查的是勾股定理,正方形的性质的运用,正方形的面积公式的运用,三角形全等的判定及性质的运用,解答时证明△ABE≌△CDB是关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
10.下列图形中,不是运用三角形的稳定性的是( )


| A. | 房屋顶支撑架 | B. | 自行车三脚架 | ||
| C. | 拉闸门 | D. | 木门上钉一根木条 |
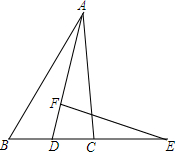 已知:AD是∠BAC的平分线,FE是AD中垂线,求证:ED2=EB•EC.
已知:AD是∠BAC的平分线,FE是AD中垂线,求证:ED2=EB•EC.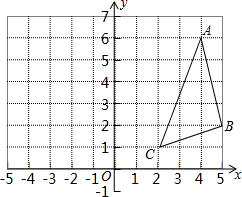 如图,△ABC的顶点坐标分别为A(4,6),B(5,2),C(2,1),
如图,△ABC的顶点坐标分别为A(4,6),B(5,2),C(2,1),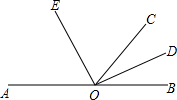 (1)已知∠AOB=30°,∠BOC=45°,则∠AOC等于15°或75°.
(1)已知∠AOB=30°,∠BOC=45°,则∠AOC等于15°或75°.