题目内容
20.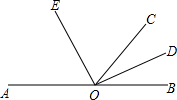 (1)已知∠AOB=30°,∠BOC=45°,则∠AOC等于15°或75°.
(1)已知∠AOB=30°,∠BOC=45°,则∠AOC等于15°或75°.(2)如图,∠BOC=60°,OE,OD分别为∠AOC和∠BOC的平分线.则∠EOD=90°.
分析 (1)分为两种情况,利当∠AOB在∠BOC的内部时,当∠AOB在∠BOC的外部时,再求出即可;
(2)先求出∠AOC,根据角平分线定义求出∠EOC和∠DOC,再求出即可.
解答 解:(1)此题要分情况:
当∠AOB在∠BOC的内部时,∠AOC=∠BOC-∠AOB=15°;
当∠AOB在∠BOC的外部时,∠AOC=∠BOC+∠AOB=75°.
故答案为:15°或75°;
(2)∵∠BOC=60°,
∴∠AOC=180°-∠BOC=120°,
∵OE,OD分别为∠AOC和∠BOC的平分线,
∴∠COE=$\frac{1}{2}$∠AOC=60°,∠DOC=$\frac{1}{2}$∠BCO=30°,
∴∠EOD=∠EOC+∠DOC=90°,
故答案为:90°.
点评 本题考查了角的有关计算和角平分线定义的应用,能求出各个角的度数是解此题的关键,此类题由于没有图形,所以要分情况讨论.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
8.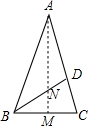 如图,已知AB=AC,AD=BD=BC,那么下列结论中,错误的是( )
如图,已知AB=AC,AD=BD=BC,那么下列结论中,错误的是( )
 如图,已知AB=AC,AD=BD=BC,那么下列结论中,错误的是( )
如图,已知AB=AC,AD=BD=BC,那么下列结论中,错误的是( )| A. | ∠BAC=36° | |
| B. | BD平分∠ABC | |
| C. | 若取BC边上的中点M,联结AM交BD于N,那么∠MNB=54° | |
| D. | 点N是BD的中点 |
5.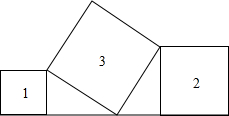 已知正方形①、②在直线上,正方形③如图放置,若正方形①、②的面积分别81cm2和144cm2,则正方形③的边长为( )
已知正方形①、②在直线上,正方形③如图放置,若正方形①、②的面积分别81cm2和144cm2,则正方形③的边长为( )
 已知正方形①、②在直线上,正方形③如图放置,若正方形①、②的面积分别81cm2和144cm2,则正方形③的边长为( )
已知正方形①、②在直线上,正方形③如图放置,若正方形①、②的面积分别81cm2和144cm2,则正方形③的边长为( )| A. | 225 | B. | 63 | C. | 50 | D. | 15 |
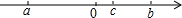 有理数a、b、c在数轴上的位置如图所示,则|a-b|-|2a-c|=a+b-c.
有理数a、b、c在数轴上的位置如图所示,则|a-b|-|2a-c|=a+b-c.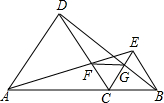 已知:如图,A、C、B在同一直线上,△ADC和△BCE都是正三角形,DB、EA分别交CE、DC于G、F.求证:
已知:如图,A、C、B在同一直线上,△ADC和△BCE都是正三角形,DB、EA分别交CE、DC于G、F.求证: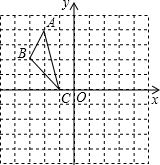 在平面直角坐标系中,△ABC的三个顶点的位置如图所示.
在平面直角坐标系中,△ABC的三个顶点的位置如图所示.