题目内容
16.若点A(3,-4)、B(-2,m)在同一个反比例函数的图象上,则m的值为6.分析 设反比例函数解析式为y=$\frac{k}{x}$,根据反比例函数图象上点的坐标特征得到k=3×(-4)=-2m,然后解关于m的方程即可.
解答 解:设反比例函数解析式为y=$\frac{k}{x}$,
根据题意得k=3×(-4)=-2m,
解得m=6.
故答案为6.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
相关题目
6.方程x2=2x的解是( )
| A. | x1=-2,x2=0 | B. | x1=$\sqrt{2}$,x2=0 | C. | x1=1,x2=2 | D. | x1=2,x2=0 |
7.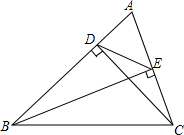 如图,△ABC中,CD⊥AB于点D,BE⊥AC于点E,连接DE,AD=2,AB=9,AC=6,下列说法正确的是( )
如图,△ABC中,CD⊥AB于点D,BE⊥AC于点E,连接DE,AD=2,AB=9,AC=6,下列说法正确的是( )
 如图,△ABC中,CD⊥AB于点D,BE⊥AC于点E,连接DE,AD=2,AB=9,AC=6,下列说法正确的是( )
如图,△ABC中,CD⊥AB于点D,BE⊥AC于点E,连接DE,AD=2,AB=9,AC=6,下列说法正确的是( )| A. | AE=3 | B. | BE=$\frac{1}{3}$$\sqrt{713}$ | C. | CE=$\frac{14}{3}$ | D. | DE=2 |
4.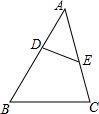 如图,在△ABC中,点D,E分别是AB,AC边上的两个点,且$\frac{AE}{AB}=\frac{AD}{AC}=\frac{1}{2}$,则S△ADE:S△ABC的值为( )
如图,在△ABC中,点D,E分别是AB,AC边上的两个点,且$\frac{AE}{AB}=\frac{AD}{AC}=\frac{1}{2}$,则S△ADE:S△ABC的值为( )
 如图,在△ABC中,点D,E分别是AB,AC边上的两个点,且$\frac{AE}{AB}=\frac{AD}{AC}=\frac{1}{2}$,则S△ADE:S△ABC的值为( )
如图,在△ABC中,点D,E分别是AB,AC边上的两个点,且$\frac{AE}{AB}=\frac{AD}{AC}=\frac{1}{2}$,则S△ADE:S△ABC的值为( )| A. | 1:$\sqrt{3}$ | B. | 1:2 | C. | 1:3 | D. | 1:4 |
1.下列多项式中是二次三项式的是( )
| A. | a+3b | B. | a2+2a+1 | C. | 3a+4ab2+5b | D. | a3+b3 |
8.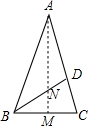 如图,已知AB=AC,AD=BD=BC,那么下列结论中,错误的是( )
如图,已知AB=AC,AD=BD=BC,那么下列结论中,错误的是( )
 如图,已知AB=AC,AD=BD=BC,那么下列结论中,错误的是( )
如图,已知AB=AC,AD=BD=BC,那么下列结论中,错误的是( )| A. | ∠BAC=36° | |
| B. | BD平分∠ABC | |
| C. | 若取BC边上的中点M,联结AM交BD于N,那么∠MNB=54° | |
| D. | 点N是BD的中点 |
5.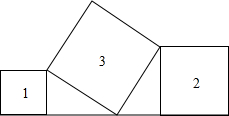 已知正方形①、②在直线上,正方形③如图放置,若正方形①、②的面积分别81cm2和144cm2,则正方形③的边长为( )
已知正方形①、②在直线上,正方形③如图放置,若正方形①、②的面积分别81cm2和144cm2,则正方形③的边长为( )
 已知正方形①、②在直线上,正方形③如图放置,若正方形①、②的面积分别81cm2和144cm2,则正方形③的边长为( )
已知正方形①、②在直线上,正方形③如图放置,若正方形①、②的面积分别81cm2和144cm2,则正方形③的边长为( )| A. | 225 | B. | 63 | C. | 50 | D. | 15 |
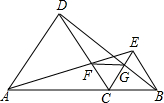 已知:如图,A、C、B在同一直线上,△ADC和△BCE都是正三角形,DB、EA分别交CE、DC于G、F.求证:
已知:如图,A、C、B在同一直线上,△ADC和△BCE都是正三角形,DB、EA分别交CE、DC于G、F.求证: