题目内容
15.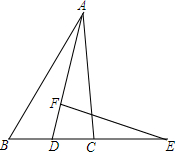 已知:AD是∠BAC的平分线,FE是AD中垂线,求证:ED2=EB•EC.
已知:AD是∠BAC的平分线,FE是AD中垂线,求证:ED2=EB•EC.
分析 连结AE,则DE=AE,再由△ACE∽△BAE,对应边成比例,即可求证.
解答  证明:连接AE,
证明:连接AE,
∵AD是角平分线,
∴∠BAD=∠CAD,
又∵EF为AD的垂直平分线,
∴AE=ED,∠DAE=∠ADE,
∴∠DAC+∠CAE=∠B+∠BAD,
∴∠CAE=∠B,
∵∠AEC=∠AEC,
∴△ACE∽△BAE,即$\frac{CE}{AE}$=$\frac{AE}{BE}$,
∴AE2=CE•BE,
即ED2=CE•BE.
点评 本题主要考查了相似三角形的判定及性质以及垂直平分线的性质问题,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
6.方程x2=2x的解是( )
| A. | x1=-2,x2=0 | B. | x1=$\sqrt{2}$,x2=0 | C. | x1=1,x2=2 | D. | x1=2,x2=0 |
7.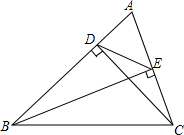 如图,△ABC中,CD⊥AB于点D,BE⊥AC于点E,连接DE,AD=2,AB=9,AC=6,下列说法正确的是( )
如图,△ABC中,CD⊥AB于点D,BE⊥AC于点E,连接DE,AD=2,AB=9,AC=6,下列说法正确的是( )
 如图,△ABC中,CD⊥AB于点D,BE⊥AC于点E,连接DE,AD=2,AB=9,AC=6,下列说法正确的是( )
如图,△ABC中,CD⊥AB于点D,BE⊥AC于点E,连接DE,AD=2,AB=9,AC=6,下列说法正确的是( )| A. | AE=3 | B. | BE=$\frac{1}{3}$$\sqrt{713}$ | C. | CE=$\frac{14}{3}$ | D. | DE=2 |
4.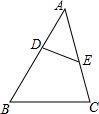 如图,在△ABC中,点D,E分别是AB,AC边上的两个点,且$\frac{AE}{AB}=\frac{AD}{AC}=\frac{1}{2}$,则S△ADE:S△ABC的值为( )
如图,在△ABC中,点D,E分别是AB,AC边上的两个点,且$\frac{AE}{AB}=\frac{AD}{AC}=\frac{1}{2}$,则S△ADE:S△ABC的值为( )
 如图,在△ABC中,点D,E分别是AB,AC边上的两个点,且$\frac{AE}{AB}=\frac{AD}{AC}=\frac{1}{2}$,则S△ADE:S△ABC的值为( )
如图,在△ABC中,点D,E分别是AB,AC边上的两个点,且$\frac{AE}{AB}=\frac{AD}{AC}=\frac{1}{2}$,则S△ADE:S△ABC的值为( )| A. | 1:$\sqrt{3}$ | B. | 1:2 | C. | 1:3 | D. | 1:4 |
5.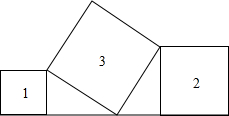 已知正方形①、②在直线上,正方形③如图放置,若正方形①、②的面积分别81cm2和144cm2,则正方形③的边长为( )
已知正方形①、②在直线上,正方形③如图放置,若正方形①、②的面积分别81cm2和144cm2,则正方形③的边长为( )
 已知正方形①、②在直线上,正方形③如图放置,若正方形①、②的面积分别81cm2和144cm2,则正方形③的边长为( )
已知正方形①、②在直线上,正方形③如图放置,若正方形①、②的面积分别81cm2和144cm2,则正方形③的边长为( )| A. | 225 | B. | 63 | C. | 50 | D. | 15 |
 直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上在原点O处的点到达点O′,点P表示的数是2.6,那么点PO′的长度是π-2.6.
直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上在原点O处的点到达点O′,点P表示的数是2.6,那么点PO′的长度是π-2.6.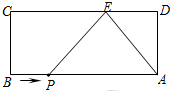 如图,长方形ABCD中,AB=9,AD=4.E为CD边上一点,CE=6.
如图,长方形ABCD中,AB=9,AD=4.E为CD边上一点,CE=6.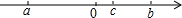 有理数a、b、c在数轴上的位置如图所示,则|a-b|-|2a-c|=a+b-c.
有理数a、b、c在数轴上的位置如图所示,则|a-b|-|2a-c|=a+b-c.