题目内容
 如图,在Rt△AOB中,O为坐标原点,∠AOB=90°,∠B=30°.若点A在反比例函数y=
如图,在Rt△AOB中,O为坐标原点,∠AOB=90°,∠B=30°.若点A在反比例函数y=| 1 |
| x |
| k |
| x |
考点:反比例函数综合题
专题:压轴题,探究型
分析:如图分别过A、B作AC⊥y轴于C,BD⊥y轴于D.设A(a,b),则ab=1.根据两角对应相等的两三角形相似,得出△OAC∽△BOD,由相似三角形的对应边成比例,则BD、OD都可用含a、b的代数式表示,从而求出BD•OD的积,进而得出结果.
解答: 解:分别过A、B作AC⊥y轴于C,BD⊥y轴于D.设A(a,b).
解:分别过A、B作AC⊥y轴于C,BD⊥y轴于D.设A(a,b).
∵点A在反比例函数y=
(x>0)的图象上,
∴ab=1.
在△OAC与△BOD中,∠AOC=90°-∠BOD=∠OBD,∠OCA=∠BDO=90°,
∴△OAC∽△BOD,
∴OC:BD=AC:OD=OA:OB,
在Rt△AOB中,∠AOB=90°,∠B=30°,
∴OA:OB=1:
,
∴b:BD=a:OD=1:
,
∴BD=
b,OD=
a,
∴BD•OD=3ab=3,
又∵点B在第四象限,
∴k=-3.
故答案为:-3.
 解:分别过A、B作AC⊥y轴于C,BD⊥y轴于D.设A(a,b).
解:分别过A、B作AC⊥y轴于C,BD⊥y轴于D.设A(a,b).∵点A在反比例函数y=
| 1 |
| x |
∴ab=1.
在△OAC与△BOD中,∠AOC=90°-∠BOD=∠OBD,∠OCA=∠BDO=90°,
∴△OAC∽△BOD,
∴OC:BD=AC:OD=OA:OB,
在Rt△AOB中,∠AOB=90°,∠B=30°,
∴OA:OB=1:
| 3 |
∴b:BD=a:OD=1:
| 3 |
∴BD=
| 3 |
| 3 |
∴BD•OD=3ab=3,
又∵点B在第四象限,
∴k=-3.
故答案为:-3.
点评:本题考查的是反比例函数综合题,涉及到相似三角形的判定与性质、反比例函数图象上点的坐标特点等知识,根据题意作出辅助线,构造出相似三角形是解答此题的关键.

练习册系列答案
相关题目
数字2012年最低工资标准将于2012年3月1日实施,深圳最低工资标准将由去年的每月1320元上涨到1500元,目前为全国最高.2010年深圳最低工资标准为1100元,假设这两年深圳的最低工资标准平均增长率为x,则关于x的方程为( )
| A、(1+x)2=1500-1100 |
| B、1100(1+x)2=1320 |
| C、1320(1+x)2=1500 |
| D、1100(1+x)2=1500 |
将一段72cm长的绳子,从一端开始每3cm作一记号,每4cm也作一记号,然后从有记号的地方剪断,则这段绳子共被剪成的段数为( )
| A、37 | B、36 | C、35 | D、34 |
 已知在平面直角系xoy中,已知直线AB:
已知在平面直角系xoy中,已知直线AB: 如图,三个大小相同的正方形重叠地放在一个大的正方形ABCD内,已知能看见的部分Ⅰ、Ⅱ、Ⅲ的面积分别是64平方厘米、38平方厘米、34平方厘米.那么正方形
如图,三个大小相同的正方形重叠地放在一个大的正方形ABCD内,已知能看见的部分Ⅰ、Ⅱ、Ⅲ的面积分别是64平方厘米、38平方厘米、34平方厘米.那么正方形 如图,已知抛物线y=ax2+bx+c经过A(1,0)、B(4,0)、C(-1,5),与y轴相交于点D,直线y=kx+m与抛物线相交于B、C两点,与y轴相交于点E.
如图,已知抛物线y=ax2+bx+c经过A(1,0)、B(4,0)、C(-1,5),与y轴相交于点D,直线y=kx+m与抛物线相交于B、C两点,与y轴相交于点E.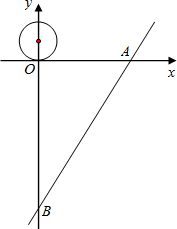 如图,在平面直角坐标系中,直线AB交x、y轴于点A(
如图,在平面直角坐标系中,直线AB交x、y轴于点A(