Question

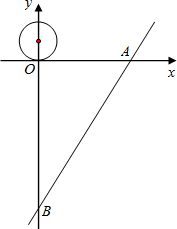如图，在平面直角坐标系中，直线AB交x、y轴于点A（10

3

，0），B（0，-30），一圆心位于（0，3），半径为3的动圆沿x轴向右滚动，动圆每6秒滚动一圈，则动圆与直线AB第一次相切时所用的时间为

 

 秒．

Answer 1

考点：圆的综合题

专题：

分析：根据题意画出图形，得出第一次与AB相切时，O正好在∠OAC的角平分线上，求出∠OAB的度数，求出∠OAM，根据三角函数值求出AM、求出OM，根据动圆每6秒滚动一圈即可求出动圆与直线AB第一次相切时所用的时间．

解答：解：
如图当⊙O于AB第一次相切时，于x轴切于M，此时O正好在∠OAC的角平分线上，
∵A（10

3

，0），B（0，-30），
∴OA=10

3

，OB=30，
∴tan∠OAB=

30

10 3

=

3

，
∴∠OAB=60°，
∴∠OAM=60°，
∵OM=3，
∴tan60°=

OM

AM

=

3

AM

，
∴AM=

3

，
∴OM=10

3

-

3

=9

3

，
设动圆与直线AB第一次相切时所用的时间是x秒，
∵动圆每6秒滚动一圈，
∴

2π×3

6

=

9 3

x

，
解得：x=

9 3

π

，
故答案为：

9 3

π

．

点评：本题考查了切线的性质，特殊角的三角函数值，圆的性质等知识点，关键是能根据题意画出图形，并知道主要应该求那一条线段的长，题目比较难懂，是有一定难度的题目．