��Ŀ����
7��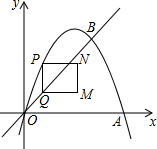 ��ͼ����ƽ��ֱ������ϵ�У�������y=-x2+3x��x�ύ��O��A���㣬��ֱ��y=x����O��B���㣬��A��B������ֱ�Ϊ��3��0������2��2������P���������ϣ��Ҳ����O��B�غϣ�����P��y���ƽ���߽�����OB�ڵ�Q����PQΪ��������PQMN��MN���Bʼ����PQͬ�࣬��PN=1�����P�ĺ�����Ϊm��m��0��������PQMN���ܳ�ΪC��
��ͼ����ƽ��ֱ������ϵ�У�������y=-x2+3x��x�ύ��O��A���㣬��ֱ��y=x����O��B���㣬��A��B������ֱ�Ϊ��3��0������2��2������P���������ϣ��Ҳ����O��B�غϣ�����P��y���ƽ���߽�����OB�ڵ�Q����PQΪ��������PQMN��MN���Bʼ����PQͬ�࣬��PN=1�����P�ĺ�����Ϊm��m��0��������PQMN���ܳ�ΪC����1���ú�m�Ĵ���ʽ��ʾ��P�����꣮
��2����C��m֮��ĺ�����ϵʽ��
��3��������PQMN��������ʱ����m��ֵ��
��4��ֱ��д������PQMN�ı�������������������ʱm��ȡֵ��Χ��
���� ��1����x=m����y=ax2+bx��������������꣮
��2���ֱ��������PQMN���ܳ�C��m֮��ĺ�����ϵʽ���ɣ�
��3�������������г����̼��ɽ����
��4�������������ʾ��P�ĺ����꼴�ɣ�
���  �⣺��1����P��������y=-x2+3x�ϣ��ҵ�P�ĺ�����Ϊm��m��0����
�⣺��1����P��������y=-x2+3x�ϣ��ҵ�P�ĺ�����Ϊm��m��0����
���P����������m��-m2+3m��
��2����PQ��y�ᣬ
��Q��m��m����
��MN���Bʼ����PQͬ�࣬��PN=1�����P�ĺ�����Ϊm��m��0����
��0��m��2ʱ����ͼ1�У�
PQ=-m2+3m-m=-m2-2m��
C=2��-m2+2m��+2=-2m2+4m+2��
��3���߾���PQMN�������Σ�
��PQ=PN=1�� ��0��m��2ʱ����ͼ3�У�
��0��m��2ʱ����ͼ3�У�
-m2+2m=1�����m1=m2=1��
��m��2ʱ����ͼ4�У�
m2-2m=1��
���m1=1+$\sqrt{2}$��m2=1-$\sqrt{2}$������������������
��4����ͼ3��֪��m=1ʱ����PQMN�ı������������������㣻
��������y=-x2+3x=-��x-$\frac{3}{2}$��2+$\frac{9}{4}$
�ඥ�������Ϊ��$\frac{3}{2}$��$\frac{9}{4}$����
��M������������ʱ����Q��m��m����
��M��m+1��m+1����
��m+1=-��m+1��2+3��m+1����
���m=2��
�൱$\frac{3}{2}$��m��2ʱ����PQMN�ı������������������㣻
��Q��������Ϊ$\frac{9}{4}$ʱ��Q�ĺ�����Ϊ$\frac{9}{4}$��
���ʱP�ĺ�����Ϊ$\frac{9}{4}$��
�൱m��$\frac{9}{4}$ʱ����PQMN�ı������������������㣻
���ϣ���m=1��$\frac{3}{2}$��m��2��m��$\frac{9}{4}$ʱ����PQMN�ı������������������㣮
���� ���⿼����κ����ۺ��⡢���Ρ������ε��й����ʣ�ѧ���ô���ϵ��������κ�������ʽ��ѧ��ֶ����۵�˼�룬��Ҫ��ȷ����ͼ�Σ��÷��̵�˼�������⣬�����ν�ϵĺ���Ŀ�������п�ѹ���⣮

 ��У����ϵ�д�
��У����ϵ�д�| A�� | ab��0 | B�� | a-b��0 | C�� | a2+b��0 | D�� | a+b��0 |
| AQIָ�� | �����ȼ� | �������죩 |
| 0-50 | �� | m |
| 51-100 | �� | 44 |
| 101-150 | �����Ⱦ | n |
| 151-200 | �ж���Ⱦ | 4 |
| 201-300 | �ض���Ⱦ | 2 |
| 300���� | ������Ⱦ | 2 |
��2����ȫ����ͳ��ͼ����ͨ��������Ƹ��г���ȫ����������ȼ�Ϊ���š��͡������������������죿
��3���ݵ��飬������Ⱦ��2�췢���ڴ����ڼ䣬ȼ���̻������Ϊ������Ⱦ��һ����Ҫԭ�ݴˣ��������һ�����������飮

| ��Ա | �� | �� | �� | �� | �� | ƽ���ɼ� |
| �ɼ� | 91 | 89 | �� | 90 | 92 | 90 |
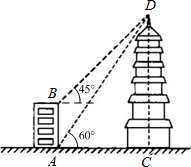 �����ķ�����λ�ڰ��ո��������ĸɵ����·�������ڿ�����ʮ���꣨1796�����ķ����������˸����ķ磬С����A���������D������Ϊ60�㣬��B���������D������Ϊ45�㣬����A��C����ֱ�λ��B��D�������·�����A��C������ͬһˮƽ���ϣ���֪AB��Ϊ13.5�ף����н���CD�ĸ߶ȣ��������ȷ����λ��
�����ķ�����λ�ڰ��ո��������ĸɵ����·�������ڿ�����ʮ���꣨1796�����ķ����������˸����ķ磬С����A���������D������Ϊ60�㣬��B���������D������Ϊ45�㣬����A��C����ֱ�λ��B��D�������·�����A��C������ͬһˮƽ���ϣ���֪AB��Ϊ13.5�ף����н���CD�ĸ߶ȣ��������ȷ����λ��