题目内容
 在平面直角坐标系中.过一点分別作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做公正点.例如.图中过点P分別作x轴,y轴的垂线.与坐标轴围成矩形OAPB的周长与面积相等,则点P是公正点.
在平面直角坐标系中.过一点分別作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做公正点.例如.图中过点P分別作x轴,y轴的垂线.与坐标轴围成矩形OAPB的周长与面积相等,则点P是公正点.①判断点M(l,2),N(-4,4)是否为公正点,并说明理由;
②若公正点P(m,3)在直线y=-x+n(n为常数)上,求m,n的值.
考点:一次函数图象上点的坐标特征
专题:新定义
分析:(1)计算1×2≠2×(1+2),4×4=2×(4+4)即可;
(2)当m>0时,根据(m+3)×2=3m,求出a,进一步求出n;当m<0时,根据(-m+3)×2=-3m求出m进一步求出n.
(2)当m>0时,根据(m+3)×2=3m,求出a,进一步求出n;当m<0时,根据(-m+3)×2=-3m求出m进一步求出n.
解答:解:(1)∵1×2≠2×(1+2),4×4=2×(4+4),
∴点M不是和谐点,点N是和谐点.
(2)由题意得:①当m>0时,
∵y=-x+n,P(m,3),
∴3=-m+n,
∴n=m+3.
∴(m+3)×2=3m,
∴m=6,
点P(m,3)在直线 y=-x+n上,代入得:n=9
②当m<0时,(-m+3)×2=-3m,
∴m=-6,
点P(m,3)在直线y=-x+n上,代入得:n=-3,
∴a=m,n=9或m=-6,n=-3.
∴点M不是和谐点,点N是和谐点.
(2)由题意得:①当m>0时,
∵y=-x+n,P(m,3),
∴3=-m+n,
∴n=m+3.
∴(m+3)×2=3m,
∴m=6,
点P(m,3)在直线 y=-x+n上,代入得:n=9
②当m<0时,(-m+3)×2=-3m,
∴m=-6,
点P(m,3)在直线y=-x+n上,代入得:n=-3,
∴a=m,n=9或m=-6,n=-3.
点评:本题主要考查对一次函数图象上点的坐标特征,三角形的面积等知识点的理解和掌握,理解题意并根据题意进行计算是解此题的关键.

练习册系列答案
相关题目
 如图,AC∥BD,AE,BE分别平分∠CAB和∠DBA,点E在CD上.
如图,AC∥BD,AE,BE分别平分∠CAB和∠DBA,点E在CD上. 如图,△ABC是边长为4cm的等边三角形,P是△ABC内的任意一点,过点P作EF∥AB分别交AC、BC于点E、F,作GH∥BC分别交AB、AC于点G、H,作MN∥AC分别交AB、BC于点M、N.试求EF+GH+MN的值.
如图,△ABC是边长为4cm的等边三角形,P是△ABC内的任意一点,过点P作EF∥AB分别交AC、BC于点E、F,作GH∥BC分别交AB、AC于点G、H,作MN∥AC分别交AB、BC于点M、N.试求EF+GH+MN的值. 如图,在△ABC中,AB=AC=14cm,D是AB的中点,DE⊥AB交AC于点E,△EBC的周长是24cm,则BC=
如图,在△ABC中,AB=AC=14cm,D是AB的中点,DE⊥AB交AC于点E,△EBC的周长是24cm,则BC=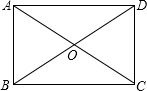 如图,矩形ABCD的对角线AC、BD的交点为O,已知BC=6cm,∠AOB=60°,则△BOC的面积为
如图,矩形ABCD的对角线AC、BD的交点为O,已知BC=6cm,∠AOB=60°,则△BOC的面积为