Question

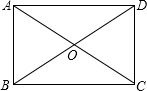如图，矩形ABCD的对角线AC、BD的交点为O，已知BC=6cm，∠AOB=60°，则△BOC的面积为

 

cm²．

Answer 1

考点：矩形的性质

专题：

分析：首先根据矩形的性质可得△BOC是等腰三角形，进而得到∠OCB=30°，再利用勾股定理计算出AB长可得△ABC的面积，然后再根据三角形的中线平分三角形的面积可得答案．

解答：解：∵四边形ABCD是矩形，
∴AO=CO=BO=DO，
∵∠AOB=60°，
∴∠OCB=30°，
∴AC=2AB，
∵BC=6cm，AB²+BC²=AC²，
∴AB=2

3

cm，
∴S_△ABC=2

3

×6×

1

2

=6

3

cm²，
∵O是AC中点，
∴△BOC的面积为：

1

2

×6

3

=3

3

cm²．
故答案为：3

3

cm²．

点评：此题主要考查了矩形的性质，关键是掌握矩形的对角线相等且互相平分．