题目内容
17.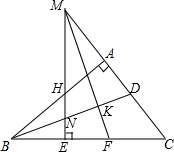 在△ABC中,∠BAC=90°,BD平分∠ABC,如图,M在CA的延长线上,ME⊥BC于E,ME分别交AB,BD于H,N,∠CME的平分线交BC于F,分别交AB,BD于G,K,求证:BD⊥MF.
在△ABC中,∠BAC=90°,BD平分∠ABC,如图,M在CA的延长线上,ME⊥BC于E,ME分别交AB,BD于H,N,∠CME的平分线交BC于F,分别交AB,BD于G,K,求证:BD⊥MF.
分析 根据∠BAC=90°,ME⊥BC,证明∠ABC=∠EMC,根据角平分线的定义证明∠CBD=∠EMF,根据垂直的定义证明结论.
解答 证明:∵∠BAC=90°,ME⊥BC,
∴∠ABC=∠EMC,又BD平分∠ABC,MF是∠CME的平分线,
∴∠CBD=∠EMF,
∵∠EMF+∠BFK=90°,
∴∠CBD+∠BFK=90°,
∴∠BKF=90°,即BD⊥MF.
点评 本题考查的是角平分线的定义和三角形内角和定理,掌握三角形内角和等于180°是解题的关键,注意垂直的概念的运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式$\sqrt{a-2}$+(b-3)2=0,(c-4)2≤0
如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式$\sqrt{a-2}$+(b-3)2=0,(c-4)2≤0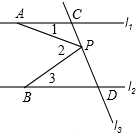 如图,直线l1∥l2,直线l3与直线l1,l2分别交于C,D两点.有一点P在C,D之间运动(不与C,D两点重合),在它运动的过程中,∠1+∠3=∠2这一相等关系是否始终成立?试说明理由.
如图,直线l1∥l2,直线l3与直线l1,l2分别交于C,D两点.有一点P在C,D之间运动(不与C,D两点重合),在它运动的过程中,∠1+∠3=∠2这一相等关系是否始终成立?试说明理由.