ĢāÄæÄŚČŻ
ČēĶ¼£¬Å×ĪļĻßy=©
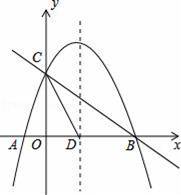
 x2+mx+nÓėxÖį½»ÓŚA”¢BĮ½µć£¬ÓėyÖį½»ÓŚµćC£¬Å×ĪļĻߵĶŌ³ĘÖį½»xÖįÓŚµćD£¬ŅŃÖŖA£Ø©1£¬0£©£¬C£Ø0£¬2£©£®
x2+mx+nÓėxÖį½»ÓŚA”¢BĮ½µć£¬ÓėyÖį½»ÓŚµćC£¬Å×ĪļĻߵĶŌ³ĘÖį½»xÖįÓŚµćD£¬ŅŃÖŖA£Ø©1£¬0£©£¬C£Ø0£¬2£©£®
£Ø1£©ĒóÅ×ĪļĻߵıķ“ļŹ½£»
£Ø2£©ŌŚÅ×ĪļĻߵĶŌ³ĘÖįÉĻŹĒ·ń“ęŌŚµćP£¬Ź¹”÷PCDŹĒŅŌCDĪŖŃüµÄµČŃüČż½ĒŠĪ£æČē¹ū“ęŌŚ£¬Ö±½ÓŠ“³öPµćµÄ×ų±ź£»Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£»
£Ø3£©µćEŹĒĻ߶ĪBCÉĻµÄŅ»øö¶Æµć£¬¹żµćE×÷xÖįµÄ“¹ĻßÓėÅ×ĪļĻßĻą½»ÓŚµćF£¬µ±µćEŌĖ¶Æµ½Ź²Ć“Ī»ÖĆŹ±£¬ĖıߊĪCDBFµÄĆ껿×ī“ó£æĒó³öĖıߊĪCDBFµÄ×ī“óĆ껿¼°“ĖŹ±EµćµÄ×ų±ź£®

””
”¾æ¼µć”涞“ĪŗÆŹż×ŪŗĻĢā£®
”¾×ØĢā”æ×ŪŗĻĢā£®
”¾·ÖĪö”æ£Ø1£©Ö±½Ó°ŃAµćŗĶCµć×ų±ź“śČėy=©
 x2+mx+nµĆm”¢nµÄ·½³Ģ×é£¬Č»ŗó½ā·½³Ģ×éĒó³öm”¢n¼“æɵƵ½Å×ĪļĻß½āĪöŹ½£»
x2+mx+nµĆm”¢nµÄ·½³Ģ×é£¬Č»ŗó½ā·½³Ģ×éĒó³öm”¢n¼“æɵƵ½Å×ĪļĻß½āĪöŹ½£»
£Ø2£©ĻČĄūÓĆÅ×ĪļĻ߶Ō³ĘÖį·½³ĢĒó³öÅ×ĪļĻߵĶŌ³ĘÖįĪŖÖ±Ļßx=©
 £¬ŌņD£Ø
£¬ŌņD£Ø
 £¬0£©£¬ŌņĄūÓĆ¹“¹É¶ØĄķ¼ĘĖć³öCD=
£¬0£©£¬ŌņĄūÓĆ¹“¹É¶ØĄķ¼ĘĖć³öCD=
 £¬Č»ŗó·ÖĄąĢÖĀŪ£ŗČēĶ¼1£¬µ±CP=CDŹ±£¬ĄūÓƵČŃüČż½ĒŠĪµÄŠŌÖŹŅ×µĆP1£Ø
£¬Č»ŗó·ÖĄąĢÖĀŪ£ŗČēĶ¼1£¬µ±CP=CDŹ±£¬ĄūÓƵČŃüČż½ĒŠĪµÄŠŌÖŹŅ×µĆP1£Ø
 £¬4£©£»µ±DP=DCŹ±£¬Ņ×µĆP2£Ø
£¬4£©£»µ±DP=DCŹ±£¬Ņ×µĆP2£Ø
 £¬
£¬
 £©£¬P3£Ø
£©£¬P3£Ø
 £¬©
£¬©
 £©£»
£©£»
£Ø3£©ĻČøł¾ŻÅ×ĪļĻßÓėxÖįµÄ½»µćĪŹĢāĒó³öB£Ø4£¬0£©£¬ŌŁĄūÓĆ“ż¶ØĻµŹż·ØĒó³öÖ±ĻßBCµÄ½āĪöŹ½ĪŖy=©
 x+2£¬ĄūÓĆŅ»“ĪŗÆŹżĶ¼ĻóÉĻµćµÄ×ų±źĢŲÕ÷ŗĶ¶ž“ĪŗÆŹżĶ¼ĻóÉĻµćµÄ×ų±źĢŲÕ÷£¬ÉčE£Øx£¬©
x+2£¬ĄūÓĆŅ»“ĪŗÆŹżĶ¼ĻóÉĻµćµÄ×ų±źĢŲÕ÷ŗĶ¶ž“ĪŗÆŹżĶ¼ĻóÉĻµćµÄ×ų±źĢŲÕ÷£¬ÉčE£Øx£¬©
 x+2£©£Ø0”Üx”Ü4£©£¬ŌņF£Øx£¬©
x+2£©£Ø0”Üx”Ü4£©£¬ŌņF£Øx£¬©
 x2+
x2+
 x+2£©£¬ŌņFE=©
x+2£©£¬ŌņFE=©
 x2+2x£¬ÓÉÓŚ”÷BEFŗĶ”÷CEF¹²µ×±ß£¬øßµÄŗĶĪŖ4£¬ŌņS”÷BCF=S”÷BEF+S”÷CEF=
x2+2x£¬ÓÉÓŚ”÷BEFŗĶ”÷CEF¹²µ×±ß£¬øßµÄŗĶĪŖ4£¬ŌņS”÷BCF=S”÷BEF+S”÷CEF=
 •4•EF=©x2+4x£¬¼ÓÉĻS”÷BCD=
•4•EF=©x2+4x£¬¼ÓÉĻS”÷BCD=
 £¬ĖłŅŌSĖıߊĪCDBF=S”÷BCF+S”÷BCD=©x2+4x+
£¬ĖłŅŌSĖıߊĪCDBF=S”÷BCF+S”÷BCD=©x2+4x+
 £Ø0”Üx”Ü4£©£¬Č»ŗóøł¾Ż¶ž“ĪŗÆŹżµÄŠŌÖŹĒóĖıߊĪCDBFµÄĆ껿×ī“󣬲¢µĆµ½“ĖŹ±Eµć×ų±ź£®
£Ø0”Üx”Ü4£©£¬Č»ŗóøł¾Ż¶ž“ĪŗÆŹżµÄŠŌÖŹĒóĖıߊĪCDBFµÄĆ껿×ī“󣬲¢µĆµ½“ĖŹ±Eµć×ų±ź£®
”¾½ā“š”æ½ā£ŗ£Ø1£©°ŃA£Ø©1£¬0£©£¬C£Ø0£¬2£©“śČėy=©
 x2+mx+nµĆ
x2+mx+nµĆ
 £¬½āµĆ
£¬½āµĆ
 £¬
£¬
”ąÅ×ĪļĻß½āĪöŹ½ĪŖy=©
 x2+
x2+
 x+2£»
x+2£»
£Ø2£©“ęŌŚ£®
Å×ĪļĻߵĶŌ³ĘÖįĪŖÖ±Ļßx=©
 =
=
 £¬
£¬
ŌņD£Ø
 £¬0£©£¬
£¬0£©£¬
”ąCD=
 =
=
 =
=
 £¬
£¬
ČēĶ¼1£¬µ±CP=CDŹ±£¬ŌņP1£Ø
 £¬4£©£»
£¬4£©£»
µ±DP=DCŹ±£¬ŌņP2£Ø
 £¬
£¬
 £©£¬P3£Ø
£©£¬P3£Ø
 £¬©
£¬©
 £©£¬
£©£¬
×ŪÉĻĖłŹö£¬Āś×ćĢõ¼žµÄPµć×ų±źĪŖ£Ø
 £¬4£©»ņ£Ø
£¬4£©»ņ£Ø
 £¬
£¬
 £©»ņ£Ø
£©»ņ£Ø
 £¬©
£¬©
 £©£»
£©£»
£Ø3£©µ±y=0Ź±£¬=©
 x2+
x2+
 x+2=0£¬½āµĆx1=©1£¬x2=4£¬ŌņB£Ø4£¬0£©£¬
x+2=0£¬½āµĆx1=©1£¬x2=4£¬ŌņB£Ø4£¬0£©£¬
ÉčÖ±ĻßBCµÄ½āĪöŹ½ĪŖy=kx+b£¬
°ŃB£Ø4£¬0£©£¬C£Ø0£¬2£©“śČėµĆ
 £¬½āµĆ
£¬½āµĆ
 £¬
£¬
”ąÖ±ĻßBCµÄ½āĪöŹ½ĪŖy=©
 x+2£¬
x+2£¬
ÉčE£Øx£¬©
 x+2£©£Ø0”Üx”Ü4£©£¬ŌņF£Øx£¬©
x+2£©£Ø0”Üx”Ü4£©£¬ŌņF£Øx£¬©
 x2+
x2+
 x+2£©£¬
x+2£©£¬
”ąFE=©
 x2+
x2+
 x+2©£Ø©
x+2©£Ø©
 x+2£©=©
x+2£©=©
 x2+2x£¬
x2+2x£¬
”ßS”÷BCF=S”÷BEF+S”÷CEF=
 •4•EF=2£Ø©
•4•EF=2£Ø©
 x2+2x£©=©x2+4x£¬
x2+2x£©=©x2+4x£¬
¶ųS”÷BCD=
 ”Į2”Į£Ø4©
”Į2”Į£Ø4©
 £©=
£©=
 £¬
£¬
”ąSĖıߊĪCDBF=S”÷BCF+S”÷BCD
=©x2+4x+
 £Ø0”Üx”Ü4£©£¬
£Ø0”Üx”Ü4£©£¬
=©£Øx©2£©2+

µ±x=2Ź±£¬SĖıߊĪCDBFÓŠ×ī“óÖµ£¬×ī“óÖµĪŖ
 £¬“ĖŹ±Eµć×ų±źĪŖ£Ø2£¬1£©£®
£¬“ĖŹ±Eµć×ų±źĪŖ£Ø2£¬1£©£®




”¾µćĘĄ”æ±¾Ģāæ¼²éĮĖ¶ž“ĪŗÆŹżµÄ×ŪŗĻĢā£ŗŹģĮ·ÕĘĪÕ¶ž“ĪŗÆŹżĶ¼ĻóÉĻµćµÄ×ų±źĢŲÕ÷”¢Ņ»“ĪŗÆŹżĶ¼ĻóÉĻµćµÄ×ų±źĢŲÕ÷ŗĶ¶ž“ĪŗÆŹżµÄŠŌÖŹ£»»įĄūÓĆ“ż¶ØĻµŹż·ØĒóŗÆŹżµÄ½āĪöŹ½£»Ąķ½ā×ų±źÓėĶ¼ŠĪŠŌÖŹ£»Įé»īÓ¦ÓĆČż½ĒŠĪµÄĆ껿¹«Ź½£»Ń§»įŌĖÓĆ·ÖĄąĢÖĀŪµÄĖ¼Ļė½ā¾öŹżŃ§ĪŹĢā£®

 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø


 C'µÄĆ껿ŹĒ
C'µÄĆ껿ŹĒ £¬ŌņcosBµÄÖµŹĒ
£¬ŌņcosBµÄÖµŹĒ 
 B£®
B£®
 C£®
C£®
 D£®
D£®


 +
+
 £©”Ā
£©”Ā
 £¬ĘäÖŠx=
£¬ĘäÖŠx=
 ©1£®
©1£®