题目内容
16.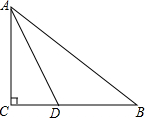 如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,D为BC边上一点,沿直线AD折叠,点C刚好落在AB边上,则△ABD的面积等于15cm2.
如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,D为BC边上一点,沿直线AD折叠,点C刚好落在AB边上,则△ABD的面积等于15cm2.
分析 根据折叠的性质可得AC=AE=6,CD=DE,∠ACD=∠AED=∠DEB=90°,利用勾股定理列式求出AB,从而求出BE,设CD=DE=x,表示出BD,然后在Rt△DEB中,利用勾股定理列式计算可求得DE=3,最后利用三角形的面积公式求解即可.
解答 解:如图所示:点C略在点E处.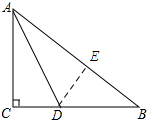
∵△ACD与△AED关于AD成轴对称,
∴AC=AE=6cm,CD=DE,∠ACD=∠AED=∠DEB=90°,
在Rt△ABC中,AB2=AC2+BC2=62+82 =102,
∴AB=10,
BE=AB-AE=10-6=4,
设CD=DE=xcm,则DB=BC-CD=8-x,
在Rt△DEB中,由勾股定理,得x2+42=(8-x)2,
解得x=3,
∴DE=3.
∴${S}_{△ADB}=\frac{1}{2}AB•DE=\frac{1}{2}×10×3$=15cm2.
故答案为:15cm2.
点评 本题考查了翻折变换的性质,勾股定理的应用,熟记性质并表示出Rt△DEB的三边,然后利用勾股定理列出方程是解题的关键.

练习册系列答案
相关题目
4.为美化市容,园林部门决定利用现有的3600盆甲种花卉和2900盆乙种花卉搭配A,B两种园艺造型共50个,摆放在文庙广场,搭配每个造型所需花卉情况如表,解答问题:
(1)符合题意的搭配方案有哪几种?
(2)若搭配一个A种造型的成本为1000元,搭配一个B种造型的成本为1200元,试说明选用哪种方案成本最低?
| 造型 | 甲 | 乙 |
| A | 90盆 | 30盆 |
| B | 40盆 | 100盆 |
(2)若搭配一个A种造型的成本为1000元,搭配一个B种造型的成本为1200元,试说明选用哪种方案成本最低?
11.如果关于x的方程(m-2)${x}^{{m}^{2}-2}$-2x-12=0是关于x的一元二次方程,那么m的值为( )
| A. | ±2 | B. | 2 | C. | -2 | D. | 都不对 |
1.下列图形中既是轴对称图形,又是旋转对称图形的是( )


| A. | ①② | B. | ①②③ | C. | ②③④ | D. | ①②③④ |
5.一元二次方程x2+x-2=0的两根是( )
| A. | x1=1,x2=2 | B. | x1=-1,x2=-2 | C. | x1=1,x2=-2 | D. | x1=-1,x2=2 |
6.下列比较两数大小,正确的是( )
| A. | 2>|-3| | B. | -$\frac{2}{3}$>-$\frac{7}{9}$ | C. | -5>-4 | D. | -3>-$\frac{1}{2}$ |
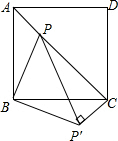 如图所示,点P是正方形ABCD内的一点,连接AP,BP,CP,将△PAB绕着点B顺时针旋转90°到△P′CB的位置.若AP=2,BP=4,∠APB=135°,求PP′及PC的长.
如图所示,点P是正方形ABCD内的一点,连接AP,BP,CP,将△PAB绕着点B顺时针旋转90°到△P′CB的位置.若AP=2,BP=4,∠APB=135°,求PP′及PC的长.