题目内容
8.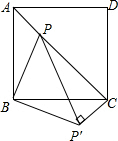 如图所示,点P是正方形ABCD内的一点,连接AP,BP,CP,将△PAB绕着点B顺时针旋转90°到△P′CB的位置.若AP=2,BP=4,∠APB=135°,求PP′及PC的长.
如图所示,点P是正方形ABCD内的一点,连接AP,BP,CP,将△PAB绕着点B顺时针旋转90°到△P′CB的位置.若AP=2,BP=4,∠APB=135°,求PP′及PC的长.
分析 先根据旋转的性质得到BP′=BP=4,P′C=AP=2,∠PBP′=90°,∠BP′C=∠BPA=135°,则可判断△PB P′是等腰直角三角形,根据等腰直角三角形的性质得PP′=$\sqrt{2}$BP=4$\sqrt{2}$,∠BP′P=45°,于是可计算出∠PP′C=90°,然后在Rt△PP′C中利用勾股定理计算PC的长.
解答 解:∵△PAB绕着点B顺时针旋转90°到△P′CB的位置,
∴BP′=BP=4,P′C=AP=2,∠PBP′=90°,∠BP′C=∠BPA=135°,
∴△PB P′是等腰直角三角形,
∴PP′=$\sqrt{2}$BP=4$\sqrt{2}$,∠BP′P=45°,
∴∠PP′C=∠BP′C-∠BP′P=135°-45°=90°,
在Rt△PP′C中,PC=$\sqrt{PP{′}^{2}+P′{C}^{2}}$=$\sqrt{(4\sqrt{2})^{2}+{2}^{2}}$=6.
答:PP′和PC的长分别为4$\sqrt{2}$,6.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.本题的关键是证明△PB P′是等腰直角三角形.

练习册系列答案
相关题目
3.抛物线y=2x2-8x-6的顶点坐标是( )
| A. | (-2,-14) | B. | (-2,14) | C. | (2,14) | D. | (2,-14) |
17.为了了解兰溪市2015年中考数学学科各分数段成绩分布情况,从中抽取1500名考生的中考数学成绩进行统计分析.在这个问题中,样本是指( )
| A. | 兰溪市2013年中考数学成绩 | |
| B. | 被抽取的1500名考生 | |
| C. | 被抽取的1500名考生的中考数学成绩 | |
| D. | 1500 |
18.有8筐白菜,以每筐25千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:
①这8筐白菜中,最接近25千克标准的是第几筐?重多少千克?
②以每筐25千克为标准,这8筐白菜总计超过多少千克或不足多少千克?
③若白菜每千克售价2.6元,则出售这8筐白菜可卖多少钱?
| 筐 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 超过或不足数(千克) | +1.5 | -3 | +2 | -0.5 | +1 | -2 | -2 | -2.5 |
②以每筐25千克为标准,这8筐白菜总计超过多少千克或不足多少千克?
③若白菜每千克售价2.6元,则出售这8筐白菜可卖多少钱?
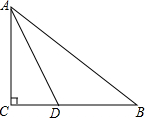 如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,D为BC边上一点,沿直线AD折叠,点C刚好落在AB边上,则△ABD的面积等于15cm2.
如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,D为BC边上一点,沿直线AD折叠,点C刚好落在AB边上,则△ABD的面积等于15cm2.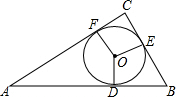 如图,在Rt△ABC中,∠C=90°,⊙O是△ABC的内切圆,切点D、E、F,
如图,在Rt△ABC中,∠C=90°,⊙O是△ABC的内切圆,切点D、E、F,