题目内容
16.先化简,再求值:$\frac{{{a^2}-4}}{{{a^2}+6a+9}}÷\frac{a-2}{a+3}-\frac{a}{a+3}$,其中a=-1.分析 原式第一项利用除法法则变形,约分后利用同分母分式的减法法则计算得到最简结果,把a的值代入计算即可求出值.
解答 解:原式=$\frac{(a+2)(a-2)}{(a+3)^{2}}$•$\frac{a+3}{a-2}$-$\frac{a}{a+3}$=$\frac{a+2}{a+3}$-$\frac{a}{a+3}$=$\frac{2}{a+3}$,
当a=-1时,原式=$\frac{2}{-1+3}$=1.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.矩形具有而一般平行四边形不一定具有的性质是( )
| A. | 对角线平行且相等 | B. | 对角线互相平分 | ||
| C. | 任意两个邻角互补 | D. | 对角互补 |
7.下列各式的运算结果为a6的是( )
| A. | a9÷a3 | B. | (a3)3 | C. | a2•a3 | D. | a3+a3 |
 如图,在四边形ABCD中,∠B=40°,∠A=140°,∠D=40°.求证:四边形ABCD是平行四边形.
如图,在四边形ABCD中,∠B=40°,∠A=140°,∠D=40°.求证:四边形ABCD是平行四边形. 由6个完全相同的小正方体搭成的几何体如图所示,它的主视图是( )
由6个完全相同的小正方体搭成的几何体如图所示,它的主视图是( )



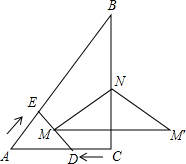 如图,△ABC中,∠C=90°,AC=3,BC=4.点D从C点出发沿射线CA以每秒1个单位长度的速度匀速运动,同时点E从A点出发沿AB以每秒1个单位长度的速度向B点匀速运动,当点E到达B点时D、E都停止运动.点M是DE的中点,直线MN⊥DE交直线BC于点N,点M′与M点关于直线BC对称.点D、E的运动时间为t(秒).
如图,△ABC中,∠C=90°,AC=3,BC=4.点D从C点出发沿射线CA以每秒1个单位长度的速度匀速运动,同时点E从A点出发沿AB以每秒1个单位长度的速度向B点匀速运动,当点E到达B点时D、E都停止运动.点M是DE的中点,直线MN⊥DE交直线BC于点N,点M′与M点关于直线BC对称.点D、E的运动时间为t(秒).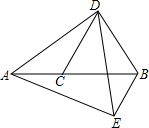 如图,C是线段AB上的点,△CDB和△ADE分别是边长为2和3等边三角形,则△ABE的面积是$\frac{5\sqrt{3}}{4}$.
如图,C是线段AB上的点,△CDB和△ADE分别是边长为2和3等边三角形,则△ABE的面积是$\frac{5\sqrt{3}}{4}$.