题目内容
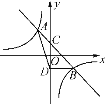
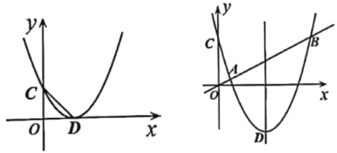
【题目】已知:函数![]() 的图象与
的图象与![]() 轴相交于点
轴相交于点![]() 两点
两点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,
,![]() .
.
(1)求抛物线的解析式且写出其顶点坐标;
(2)连结![]() ,求
,求![]() 的值.
的值.
【答案】(1)抛物线的解析式![]() ,顶点坐标
,顶点坐标![]() ;(2)
;(2)![]() .
.
【解析】
(1)函数与x轴相交于点A(x1,0),B(x2,0)两点,则x1,x2,满足y=0时,方程的根与系数关系.因为x1+x2=2,则可求b,再根据抛物线与y轴的交点为C(0,3),则可求出c,从而求得抛物线解析式.
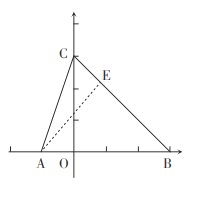
(2)已知解析式则可得A,B,C坐标,求sin∠ACB,须作垂线构造直角三角形,结论易得.
解:(1)∵函数与![]() 轴相交于点
轴相交于点![]() ,
,![]() 两点,
两点,
![]()
![]() 为
为![]() 的两个根,
的两个根,
![]()
![]() ,即:
,即:![]()
∵函数![]() 的图像与
的图像与![]() 轴相交于点
轴相交于点![]()
![]()
![]()
![]() 所求抛物线的解析式
所求抛物线的解析式![]() ,顶点坐标
,顶点坐标![]()
(2)令![]() ,解得
,解得![]() 或
或![]() .
.
又![]() ,
,
![]()
![]() ,
,![]()
根据题意画图,过点![]() 作
作![]() 于点
于点![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
![]()
![]() 为等腰直角三角形,
为等腰直角三角形,
![]()
![]() ,
,
![]()
![]() 为等腰直角三角形,
为等腰直角三角形,
设![]() ,则
,则![]() ,
,
∵![]() ,
, ![]()
![]() ,
, ![]()
![]() ,即
,即![]() .
.
在![]() 中,
中,![]() ,
,![]() ,则
,则![]() 。
。
![]()
![]() .
.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案【题目】为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
选择意向 | 所占百分比 |
文学鉴赏 | a |
科学实验 | 35% |
音乐舞蹈 | b |
手工编织 | 10% |
其他 | c |

根据统计图表中的信息,解答下列问题:
(1)本次调查的学生总人数为 ;
(2)补全条形统计图;
(3)将调查结果绘成扇形统计图,则“音乐舞蹈”社团所在扇形所对应的圆心角为 ;
(4)若该校共有1200名学生,试估计全校选择“科学实验”社团的学生人数为 .
【题目】随着国内疫情基本得到控制,旅游业也慢慢复苏,经市场调研发现旅游景点未来![]() 天内,旅游人数
天内,旅游人数![]() 与时间
与时间![]() 的关系如下表;每张门票
的关系如下表;每张门票![]() 与时间
与时间![]() 之间存在如下图所示的一次函数关系.(
之间存在如下图所示的一次函数关系.(![]() ,且
,且![]() 为整数)
为整数)
时间 |
|
|
|
|
|
人数 |
|
|
|
|
|
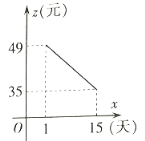
请结合上述信息解决下列问题:
(1)直接写出:![]() 关于
关于![]() 的函数关系式是 .
的函数关系式是 .![]() 与时间
与时间![]() 函数关系式是 .
函数关系式是 .
(2)请预测未来![]() 天中哪一天的门票收入最多,最多是多少?
天中哪一天的门票收入最多,最多是多少?
(3)为支援武汉抗疫,该旅游景点决定从每天获得的门票收入中拿出![]() 元捐赠给武汉红十字会,求捐款后共有几天每天剩余门票收入不低于
元捐赠给武汉红十字会,求捐款后共有几天每天剩余门票收入不低于![]() 元?
元?