题目内容
19. 如图,AB是⊙O的直径,CD为弦,且AB⊥CD,垂足是点E,已知∠COB=60°,则∠DAB的度数为( )
如图,AB是⊙O的直径,CD为弦,且AB⊥CD,垂足是点E,已知∠COB=60°,则∠DAB的度数为( )| A. | 60° | B. | 30° | C. | 25° | D. | 35° |
分析 根据垂径定理可得$\widehat{CB}$=$\widehat{BD}$,进而可得∠DAB=$\frac{1}{2}$∠COB,然后再根据∠COB=60°,可得∠DAB的度数.
解答 解:∵AB⊥CD,AB是⊙O的直径,
∴$\widehat{CB}$=$\widehat{BD}$,
∴∠DAB=$\frac{1}{2}$∠COB,
∵∠COB=60°,
∴∠DAB=30°,
故选:B.
点评 此题主要考查了垂径定理和周角定理,关键是掌握垂径定理:垂直弦的直径平分这条弦,并且平分弦所对的两条.圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
相关题目
14.在二次根式$\sqrt{2x-6}$中,x的取值范围是( )
| A. | x>3 | B. | x≥3 | C. | x≤3 | D. | x<3 |
4.下列语句中错误的是( )
| A. | 数字0是单项式 | B. | -$\frac{2ab}{3}$的系数是-$\frac{2}{3}$ | ||
| C. | $\frac{1}{2}$xy是二次单项式 | D. | 单项式-a的系数和次数都是1 |
9.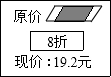 如图是某超市中“飘柔”洗发水的价格标签,一售货员不小心将墨水滴在标签上,使得原价看不清楚,请你帮忙算一算,该洗发水的原价是( )
如图是某超市中“飘柔”洗发水的价格标签,一售货员不小心将墨水滴在标签上,使得原价看不清楚,请你帮忙算一算,该洗发水的原价是( )
 如图是某超市中“飘柔”洗发水的价格标签,一售货员不小心将墨水滴在标签上,使得原价看不清楚,请你帮忙算一算,该洗发水的原价是( )
如图是某超市中“飘柔”洗发水的价格标签,一售货员不小心将墨水滴在标签上,使得原价看不清楚,请你帮忙算一算,该洗发水的原价是( )| A. | 15.36元 | B. | 16元 | C. | 24元 | D. | 23.04元 |
 如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F. 在△ABC中,AB=AC,AE=AD,且BD与CE交于点O,连AO延长交BC于F,求证:
在△ABC中,AB=AC,AE=AD,且BD与CE交于点O,连AO延长交BC于F,求证: