题目内容
10. 在△ABC中,AB=AC,AE=AD,且BD与CE交于点O,连AO延长交BC于F,求证:
在△ABC中,AB=AC,AE=AD,且BD与CE交于点O,连AO延长交BC于F,求证:(1)△ABD≌△ACE;
(2)OB=OC;
(3)AF⊥BC.
分析 (1)根据SAS证明△ABD≌△ACE即可;
(2)利用全等三角形的性质和等式的性质证明即可;
(3)根据等腰三角形的性质三线合一进行证明即可.
解答 证明:(1)在△ABD与△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AE=AD}\end{array}\right.$,
∴△ABD≌△ACE;
(2)∵△ABD≌△ACE,
∴∠ABD=∠ACE,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠OBC=∠OCB,
∴OB=OC,
(3)在△ABO与△ACO中,
$\left\{\begin{array}{l}{OB=OC}\\{∠ABO=∠ACO}\\{AB=AC}\end{array}\right.$,
∴△ABO≌△ACO,
∴∠BAF=∠CAF,
∵AB=AC,
∴AF⊥BC.
点评 此题主要考查等腰三角形的性质及全等三角形的判定与性质的综合运用,解答时证明三角形全等是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19. 如图,AB是⊙O的直径,CD为弦,且AB⊥CD,垂足是点E,已知∠COB=60°,则∠DAB的度数为( )
如图,AB是⊙O的直径,CD为弦,且AB⊥CD,垂足是点E,已知∠COB=60°,则∠DAB的度数为( )
 如图,AB是⊙O的直径,CD为弦,且AB⊥CD,垂足是点E,已知∠COB=60°,则∠DAB的度数为( )
如图,AB是⊙O的直径,CD为弦,且AB⊥CD,垂足是点E,已知∠COB=60°,则∠DAB的度数为( )| A. | 60° | B. | 30° | C. | 25° | D. | 35° |
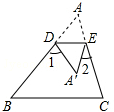 如图,D、E分别是△ABC的边AB、AC上的点,把△ADE沿DE折叠,使点A落在四边形BCED内部A′处,已知∠A=40°,则∠1+∠2=80°度.
如图,D、E分别是△ABC的边AB、AC上的点,把△ADE沿DE折叠,使点A落在四边形BCED内部A′处,已知∠A=40°,则∠1+∠2=80°度.