题目内容
8.解方程:(1)x2-2x=0;
(2)2x2+3x-1=0.
分析 (1)直接利用提取公因式法分解因式,进而解方程即可;
(2)首先判断b2-4ac的符号,再利用求根公式得出答案.
解答 解:(1)x2-2x=0
x(x-2)=0,
解得:x1=0,x2=2;
(2)2x2+3x-1=0
∵b2-4ac=9-4×2×(-1)=17,
∴x=$\frac{-3±\sqrt{17}}{4}$,
则x1=$\frac{-3+\sqrt{17}}{4}$,x2=$\frac{-3-\sqrt{17}}{4}$.
点评 此题主要考查了因式分解法以及公式法解方程,正确记忆求根公式是解题关键.

练习册系列答案
相关题目
19. 如图,AB是⊙O的直径,CD为弦,且AB⊥CD,垂足是点E,已知∠COB=60°,则∠DAB的度数为( )
如图,AB是⊙O的直径,CD为弦,且AB⊥CD,垂足是点E,已知∠COB=60°,则∠DAB的度数为( )
 如图,AB是⊙O的直径,CD为弦,且AB⊥CD,垂足是点E,已知∠COB=60°,则∠DAB的度数为( )
如图,AB是⊙O的直径,CD为弦,且AB⊥CD,垂足是点E,已知∠COB=60°,则∠DAB的度数为( )| A. | 60° | B. | 30° | C. | 25° | D. | 35° |
16. 两个反比例函数和在第一象限内的图象如图所示,点P在的图象上,PC⊥x轴于点C,交的图象于点A,PD⊥轴于点D,交的图象于点B,当点P在的图象上运动时,下列结论错误的是( )
两个反比例函数和在第一象限内的图象如图所示,点P在的图象上,PC⊥x轴于点C,交的图象于点A,PD⊥轴于点D,交的图象于点B,当点P在的图象上运动时,下列结论错误的是( )
 两个反比例函数和在第一象限内的图象如图所示,点P在的图象上,PC⊥x轴于点C,交的图象于点A,PD⊥轴于点D,交的图象于点B,当点P在的图象上运动时,下列结论错误的是( )
两个反比例函数和在第一象限内的图象如图所示,点P在的图象上,PC⊥x轴于点C,交的图象于点A,PD⊥轴于点D,交的图象于点B,当点P在的图象上运动时,下列结论错误的是( )| A. | △ODB与△OCA的面积相等 | |
| B. | 当点A是PC的中点时,点B一定是PD的中点 | |
| C. | 只有当四边形OCPD为正方形时,四边形PAOB的面积最大 | |
| D. | $\frac{CA}{PA}$=$\frac{DB}{PB}$ |
13. 数a,b在数轴上的位置如图所示,则a-b是( )
数a,b在数轴上的位置如图所示,则a-b是( )
 数a,b在数轴上的位置如图所示,则a-b是( )
数a,b在数轴上的位置如图所示,则a-b是( )| A. | 正数 | B. | 零 | C. | 负数 | D. | 都有可能 |
17.下列命题:
①负数没有立方根;
②一个实数的立方根不是正数就是负数;
③一个正数或负数的立方根与这个数的符号一致;
④如果一个数的立方根等于它本身,那么它一定是1或0.
其中正确的是( )
①负数没有立方根;
②一个实数的立方根不是正数就是负数;
③一个正数或负数的立方根与这个数的符号一致;
④如果一个数的立方根等于它本身,那么它一定是1或0.
其中正确的是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
18.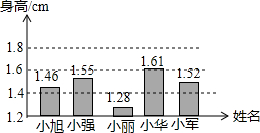 学习了统计图后,老师让小明按表提供的信息绘制统计图,小明绘制了如图所示的条形统计图.
学习了统计图后,老师让小明按表提供的信息绘制统计图,小明绘制了如图所示的条形统计图.
(1)小明绘制的统计图能反映每一位同学的身高吗?
(2)此图会使人产生错觉吗?应该怎样改动?
 学习了统计图后,老师让小明按表提供的信息绘制统计图,小明绘制了如图所示的条形统计图.
学习了统计图后,老师让小明按表提供的信息绘制统计图,小明绘制了如图所示的条形统计图.| 姓名 | 小旭 | 小强 | 小丽 | 小华 | 小军 |
| 身高/m | 1.46 | 1.55 | 1.28 | 1.61 | 1.52 |
(2)此图会使人产生错觉吗?应该怎样改动?