题目内容
5.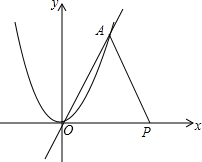 如图,抛物线y=x2与直线y=2x在第一象限内有一交点A.
如图,抛物线y=x2与直线y=2x在第一象限内有一交点A.(1)你能求出点A的坐标吗?
(2)在x轴上是否存在一点P,使△AOP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
分析 (1)利用解方程组$\left\{\begin{array}{l}{y={x}^{2}}\\{y=2x}\end{array}\right.$可得到A点坐标;
(2)需要分类讨论:AP=AO、OA=OP、AP=OP,根据等腰三角形的性质来求点P的坐标.
解答 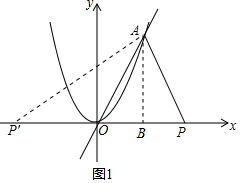 解:(1)解方程组$\left\{\begin{array}{l}{y={x}^{2}}\\{y=2x}\end{array}\right.$得$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$,
解:(1)解方程组$\left\{\begin{array}{l}{y={x}^{2}}\\{y=2x}\end{array}\right.$得$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$,
所以A点坐标为(2,4);
(2)①当AP=AO时,作AB⊥x轴于B点,如图1,
当PB=OB时,△AOP是以OP为底的等腰三角形,
而A(2,4),
所以P点坐标为(4,0).
②当OA=OP时,∵A(2,4),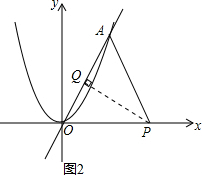
∴OA=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
则P(±2$\sqrt{5}$,0);
③当AP=OP时,如图2,过点P作PQ⊥AO于点Q.
设P(t,0).
则Q(1,2).
故$\frac{1}{2}$OA•PQ=$\frac{1}{2}$OP×4,即$\frac{1}{2}$×2$\sqrt{5}$×$\sqrt{(1-t)^{2}+{2}^{2}}$=$\frac{1}{2}$t×4,
解得t=5,
即(5,0).
综上所述,符合条件的点P的坐标是(4,0)或(2$\sqrt{5}$,0)或(-2$\sqrt{5}$,0)或(5,0).
点评 本题考查了二次函数综合题,同时在两个函数解析式上,应是这两个函数解析式的公共解.答案较多时,应有规律的去找不同的解是解题关键.

| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
| A. | (±$\frac{1}{4}$)2=$\frac{1}{2}$ | B. | ±($\sqrt{1\frac{9}{16}}$)=±1$\frac{1}{4}$ | C. | -$\sqrt{0.9}$=-0.3 | D. | $\sqrt{1{3}^{2}-{7}^{2}}$=6 |
| A. | 平行四边形的对角相等 | |
| B. | 正方形的对称轴有四条 | |
| C. | 矩形既是中心对称图形又是轴对称图形 | |
| D. | 菱形的对角线相等且互相平分 |
 抛物线y=ax2+bx+c如图所示,则此抛物线的解析式为y=-2(x-1)2+8..
抛物线y=ax2+bx+c如图所示,则此抛物线的解析式为y=-2(x-1)2+8..
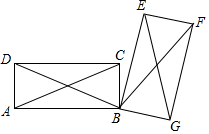 如图,把矩形ABCD绕点B顺时针旋转得到矩形EBGF,则图中与线段AC相等的线段有( )条.
如图,把矩形ABCD绕点B顺时针旋转得到矩形EBGF,则图中与线段AC相等的线段有( )条.