题目内容
1. 如图,在长方形ABCD中,AB=9,BC=15,以点B为圆心,BC长为半径画弧,交边AD于点E,则AE的长为12.
如图,在长方形ABCD中,AB=9,BC=15,以点B为圆心,BC长为半径画弧,交边AD于点E,则AE的长为12.
分析 连接BE,由圆的性质得出BE=BC=15,由矩形的性质得出∠A=90°,由勾股定理求出AE即可.
解答 解:连接BE,如图所示
则BE=BC=15,
∵四边形ABC是矩形,
∴∠A=90°,
∴AE=$\sqrt{B{E}^{2}-A{B}^{2}}$=$\sqrt{1{5}^{2}-{9}^{2}}$=12,
故答案为:12.
点评 本题考查了矩形的性质、勾股定理、圆的性质;熟练掌握矩形的性质,由勾股定理求出AE是解决问题的关键.

练习册系列答案
相关题目
11.已知圆的半径为4,一点到圆心的距离是5,则这点在( )
| A. | 圆内 | B. | 圆上 | C. | 圆外 | D. | 都有可能 |
13. 如图,△ABC是等边三角形,CB=BD,连接AD,∠ACD=110°,则∠BAD的度数为( )
如图,△ABC是等边三角形,CB=BD,连接AD,∠ACD=110°,则∠BAD的度数为( )
 如图,△ABC是等边三角形,CB=BD,连接AD,∠ACD=110°,则∠BAD的度数为( )
如图,△ABC是等边三角形,CB=BD,连接AD,∠ACD=110°,则∠BAD的度数为( )| A. | 10° | B. | 15° | C. | 20° | D. | 25° |
10.关于x的方程x2+2kx-1=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 无实数根 | D. | 不能确定 |
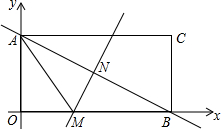 如图,长方形AOBC在直角坐标系中,点A在y轴上,点B在x轴上,已知点C的坐标是(8,4).
如图,长方形AOBC在直角坐标系中,点A在y轴上,点B在x轴上,已知点C的坐标是(8,4).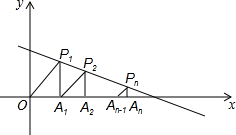 如图所示,在函数y=-$\frac{1}{3}$x+$\frac{4}{3}$(x>0)的图象上,△P1OA,△P2A1A2,△P2A2A3,…,△PnAn-1An都是等腰直角三角形,且直角边OA1,A1A2,…,An-1An都在x轴上,则An的坐标为Pn[1+$\frac{3}{4}$+$\frac{9}{16}$+…($\frac{3}{4}$)n-1,($\frac{3}{4}$)n-1].
如图所示,在函数y=-$\frac{1}{3}$x+$\frac{4}{3}$(x>0)的图象上,△P1OA,△P2A1A2,△P2A2A3,…,△PnAn-1An都是等腰直角三角形,且直角边OA1,A1A2,…,An-1An都在x轴上,则An的坐标为Pn[1+$\frac{3}{4}$+$\frac{9}{16}$+…($\frac{3}{4}$)n-1,($\frac{3}{4}$)n-1].