题目内容
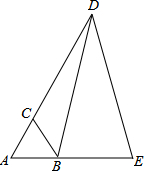 如图,等边△ABC,D、E分别在AC、AB的延长线上,且CD=AE,求证:BD=DE.
如图,等边△ABC,D、E分别在AC、AB的延长线上,且CD=AE,求证:BD=DE.考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:证明题
分析:延长AE到F,使EF=AC,连结DF,由等边三角形的性质就可以得出AC=AB=BC,∠A=∠ABC=∠ACB=60°,由等式的性质就可以得出AF=AD,得出△ADF为等边三角形,得出AD=DF,∠A=∠F=60°,得出△ADB≌△FDE就可以得出结论.
解答: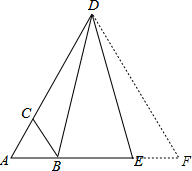 证明:延长AE到F,使EF=AC,连结DF.
证明:延长AE到F,使EF=AC,连结DF.
∵△ABC是等边三角形,
∴AC=AB=BC,∠A=∠ABC=∠ACB=60°.
∴EF=AB.
∵CD=AE,
∴CD+AC=AE+EF,
∴AD=AF.
∴△ADF为等边三角形,
∴AD=FD,∠A=∠F=60°.
在△ADB和△FDE中,
,
∴△ADB≌△FDE(SAS),
∴BD=DE.
 证明:延长AE到F,使EF=AC,连结DF.
证明:延长AE到F,使EF=AC,连结DF.∵△ABC是等边三角形,
∴AC=AB=BC,∠A=∠ABC=∠ACB=60°.
∴EF=AB.
∵CD=AE,
∴CD+AC=AE+EF,
∴AD=AF.
∴△ADF为等边三角形,
∴AD=FD,∠A=∠F=60°.
在△ADB和△FDE中,
|
∴△ADB≌△FDE(SAS),
∴BD=DE.
点评:本题考查了等边三角形的性质及判定的运用,等式的性质的运用,全等呢过三角形的判定及性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 根据数轴上a,b,c的大小关系,化简|a+b|+|b+c|-|a-c|.
根据数轴上a,b,c的大小关系,化简|a+b|+|b+c|-|a-c|.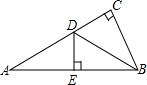 如图,在三角形ABC中,∠C=90°,BD平分∠ABC交于AC于点D,DE垂直平分AB,交AC于点D,交AB于点E,若DE=1.5cm,求AC的长.
如图,在三角形ABC中,∠C=90°,BD平分∠ABC交于AC于点D,DE垂直平分AB,交AC于点D,交AB于点E,若DE=1.5cm,求AC的长.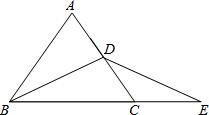 如图,在△ABC中,BA=BC,BD⊥AC,延长BC至点E,恰使CE=CD,BD=DE,求证:△ABC是等边三角形.
如图,在△ABC中,BA=BC,BD⊥AC,延长BC至点E,恰使CE=CD,BD=DE,求证:△ABC是等边三角形.