题目内容
2. 在平面直角坐标系中,已知点A(-3,2),B(-1,0),C(-2,-1).
在平面直角坐标系中,已知点A(-3,2),B(-1,0),C(-2,-1).(1)请在图中画出△ABC,并画出△ABC关于y轴对称的图形.
(2)判定△ABC的形状,并说明理由.
分析 (1)补充成网格结构,找出点A、B、C的位置,再找出点A、B、C关于y轴的对称点A′、B′、C′的位置,然后顺次连接即可;
(2)利用勾股定理列式求出AB、BC、AC,再利用勾股定理逆定理判断出三角形是直角三角形.
解答 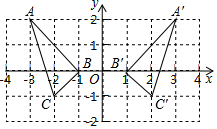 解:(1)如图所示;
解:(1)如图所示;
(2)由勾股定理得,AB=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
BC=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
AC=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∵AB2+BC2=(2$\sqrt{2}$)2+($\sqrt{2}$)2=10,
AC2=($\sqrt{10}$)2=10,
∴AB2+BC2=AC2,
∴△ABC是直角三角形.
点评 本题考查了利用轴对称变换作图,勾股定理和勾股定理逆定理,补充成网格结构并准确确定出对应点的位置是解题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
12.小马虎在下面的计算中只做对了一道题,他做对的题目是( )
| A. | $\frac{m}{a}$+$\frac{m}{b}$=$\frac{2m}{ab}$ | B. | 1-$\frac{a-1}{a}$=-$\frac{1}{a}$ | C. | ($\frac{b}{a}$)2÷($\frac{a}{b}$)2=$\frac{{b}^{4}}{{a}^{4}}$ | D. | $\frac{-x-y}{x-y}$=-1 |
10.交通运输部消息:2017年春运从1月13日开始至2月21日结束,预计此次春运客流量将达到29.78亿人次,同比增长2.2%,将29.78亿用科学记数法表示应为( )
| A. | 2.978×109 | B. | 2.978×108 | C. | 29.78×108 | D. | 0.2978×1010 |
14.一元一次不等式2(x+1)≥4的解集在数轴上表示为( )
| A. |  | B. |  | C. |  | D. |  |