题目内容

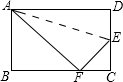如图，在矩形ABCD中，已知AB=8cm，BC=10cm，折叠矩形的一边AD，使点D落在BC边的点F处，折痕为AE，求CE的长．
考点：翻折变换（折叠问题）
专题：
分析：设CE=x，EF=8-x，在△ECF中利用勾股定理即可求得CE的长．
解答：解：设CE=x，EF=8-x，CF=
1
2
BC=5，
则在Rt△ECF中，EF2=CE2+CF2，即（8-x）2=x2+52，
解得x=
39
16
，
故CE=
39
16
cm．
点评：本题考查折叠变换和学生的逻辑思维能力，解决此类问题，应结合题意，最好实际操作图形的折叠，易于找到图形间的关系．
练习册系列答案
相关题目
已知点A(-
1
2
，y1)、B（3，y2）在二次函数y=（x-1）2-4图象上，则y1，y2大小关系
 
．
（-
5
13
）2009×（-2
3
5
）2009等于（　　）
A、-1B、1C、0D、2009
若x=2是关于x的方程2x+a=3的解，则a的值是（　　）
A、1B、-1C、5D、7
（1）计算：
(-2)2
+
327
-（
3
）2；  
（2）解方程：（x+1）2=16．
若一个角比它的补角大20°，求这个角的度数．
已知ax=3，ay=2，分别求：
①ax+y的值；
②a3x-2y的值．
解下列不等式，并把它们的解集在数轴上表示出来：
（1）3x-9≤0；
（2）2x-5＜5x-2；
（3）2（-3+x）＞3（x+2）；
（4）
x+7
2
-1＜
3x+2
2
．
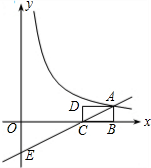如图，矩形ABCD中，AB=1，BC=2，BC在x轴上，一次函数y=kx-2的图象经过点A、C，并与y轴交于点E．反比例函数y=
m
x
的图象经过点A，并且与一次函数y=kx-2的图象交于另一点F．
（1）点C的坐标是
 
；
（2）求一次函数和反比例函数的解析式；
（3）请写出点F的坐标：
 
，并根据图象写出一次函数的值大于反比例函数的值的x的取值范围
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网