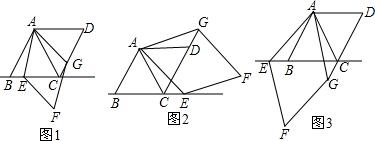
题目内容
15.由特殊到一般、类比、转化是数学学习和研究中经常用到的思想方法.下面是对一道几何题进行变式探究的思路,请你运用上述思想方法完成探究任务.问题情境:在四边形ABCD中,AC是对角线,E为边BC上一点,连接AE.以E为旋转中心,将线段AE顺时针旋转,旋转角与∠B相等,得到线段EF,连接CF.
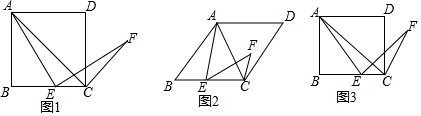
(1)特例分析:如图1,若四边形ABCD是四边形,求证:AC⊥CF;
(2)拓展分析一:如图2,若四边形ABCD是菱形,探究下列问题:
①当∠B=50°时,求∠ACF的度数;
②针对图2的条件,写出一般的结论(不必证明);
(3)拓展探究二:如图3,若四边形ABCD是矩形,且BC=k•AB(k>1).若前提条件不变,“特例分析”中得到的结论还成立吗?若成立,请证明;若不成立,修改题中的条件使结论成立(不必证明).
分析 (1)如图1中,作EH∥AC交AB于H.只要证明△HAE≌△CEF,即可推出∠AHE=∠ECF=135°,由∠BCA=45°,推出∠ACF=90°;
(2)①如图2中,作EH∥AC交AB于H.只要证明△HAE≌△CEF,即可解决问题.②∠ACF=∠B;
(3)结论:当EF=k•AE时,CF⊥AE.如图3中,作EH∥AC交AB于H,AC与EF交于点O.只要证明△HAE∽△CEF,推出∠HEA=∠F,由∠HEA=∠CAE,推出∠CAE=∠F,由∠AOE=∠FOC,∠EAO+∠AOE=90°,推出∠FOC+∠F=90°,即可得到∠OCF=90°;
解答 (1)证明:如图1中,作EH∥AC交AB于H.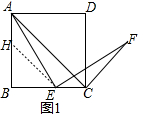
∵四边形ABCD是正方形,
∴AB=BC,∠BAC=∠BCA=45°,
∵EH∥AC,
∴∠BHE=∠BAC=45°,∠BEH=∠BCA=45°,
∴∠BHE=∠BEH=45°,∠AHE=135°,
∴BH=BE,
∴AH=CE,
∵∠AEC=∠B+∠BAE=∠AEF+∠CEF,
∵∠AEF=∠B=90°,
∴∠HAE=∠CEF,
在△HAE和△CEF中,
$\left\{\begin{array}{l}{AE=EF}\\{∠HAE=∠CEF}\\{AH=CE}\end{array}\right.$,
∴△HAE≌△CEF,
∴∠AHE=∠ECF=135°,
∵∠BCA=45°,
∴∠ACF=90°,
∴AC⊥CF.
(2)解:①如图2中,作EH∥AC交AB于H.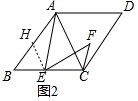
∵四边形ABCD是菱形,
∴AB=BC,∠BAC=∠BCA,
∵EH∥AC,
∴∠BHE=∠BAC,∠BEH=∠BCA,
∴∠BHE=∠BEH,
∴BH=BE,
∴AH=CE,
∵∠AEC=∠B+∠BAE=∠AEF+∠CEF,
∵∠AEF=∠B,
∴∠HAE=∠CEF,
在△HAE和△CEF中,
$\left\{\begin{array}{l}{AE=EF}\\{∠HAE=∠CEF}\\{AH=CE}\end{array}\right.$,
∴△HAE≌△CEF,
∴∠AHE=∠ECF,
∵∠B=50°,
∴∠BHE=∠ACB=65°,
∴∠AHE=∠ECF=115°
∴∠ACF=115°-65°=50°.
②结论:∠ACF=∠B.(证明方法类似①)
(3)解:结论:当EF=k•AE时,CF⊥AE.理由如下:
如图3中,作EH∥AC交AB于H,AC与EF交于点O.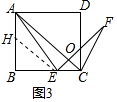
∵EH∥AC,
∴$\frac{AH}{AB}$=$\frac{EC}{CB}$,
∴$\frac{AH}{EC}$=$\frac{AB}{BC}$=$\frac{1}{K}$,
∵EF=k•AE,
∴$\frac{AH}{EC}$=$\frac{AE}{EF}$=$\frac{1}{k}$,
∵∠AEC=∠B+∠BAE=∠AEF+∠CEF,
∵∠AEF=∠B=90°,
∴∠HAE=∠CEF,
∴△HAE∽△CEF,
∴∠HEA=∠F,
∵∠HEA=∠CAE,
∴∠CAE=∠F,
∵∠AOE=∠FOC,∠EAO+∠AOE=90°,
∴∠FOC+∠F=90°,
∴∠OCF=90°,
∴AC⊥CF.
点评 本题考查四边形综合题、正方形的性质、等腰直角三角形的性质、全等三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形或相似三角形解决问题,属于中考压轴题.

 名校课堂系列答案
名校课堂系列答案| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
 实数a,b在数轴上的对应点的位置如图所示,把-a,b,0按照从小到大的顺序排列,正确的是( )
实数a,b在数轴上的对应点的位置如图所示,把-a,b,0按照从小到大的顺序排列,正确的是( )| A. | -a<b<0 | B. | 0<-a<b | C. | b<0<-a | D. | 0<b<-a |
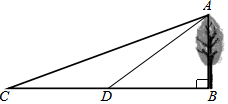 如图,为了测树AB的高,李明在C处,测得∠ACB=15°,他沿CB方向走了20米,到达D处,测得∠ADB=30°,你能帮助李明计算出树的高度为10米.
如图,为了测树AB的高,李明在C处,测得∠ACB=15°,他沿CB方向走了20米,到达D处,测得∠ADB=30°,你能帮助李明计算出树的高度为10米.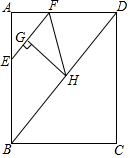 如图,在矩形ABCD中,AB=8,BC=6,点E从点A出发,以每秒4个单位长度的速度沿边AB运动,到点B停止,过点E作EF∥BD交AD于点F,把△FAE绕点F逆时针方向旋转得到△FGH,点G落在线段EF上,设点E的运动时间为t(秒)
如图,在矩形ABCD中,AB=8,BC=6,点E从点A出发,以每秒4个单位长度的速度沿边AB运动,到点B停止,过点E作EF∥BD交AD于点F,把△FAE绕点F逆时针方向旋转得到△FGH,点G落在线段EF上,设点E的运动时间为t(秒)