题目内容
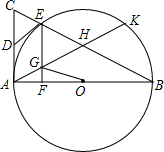 在Rt△ABC中,∠BAC=90°,以AB为直径⊙O交BC于点E,D为AC中点,EF⊥AB于点F.过A作AK∥DE交⊙O于K,交BC于H,交EF于G.
在Rt△ABC中,∠BAC=90°,以AB为直径⊙O交BC于点E,D为AC中点,EF⊥AB于点F.过A作AK∥DE交⊙O于K,交BC于H,交EF于G.(1)求证:DE是⊙O的切线;
(2)已知EG=2GF,OG=2,求△AKB的面积.
考点:切线的判定
专题:数形结合
分析:(1)首先连接AE,OE,由以AB为直径⊙O交BC于点E,D为AC中点,易得AD=DE,又由OA=OE,可得∠OED=∠CAB=90°,即可证得DE是⊙O的切线;
(2)易得四边形ADEG是菱形,由EG=2GF,可得△OAE是等边三角形,继而求得线段AK与BK的长,则可求得△AKB的面积.
(2)易得四边形ADEG是菱形,由EG=2GF,可得△OAE是等边三角形,继而求得线段AK与BK的长,则可求得△AKB的面积.
解答:(1)证明:连接AE,OE,
∵AB是⊙O直径,
∴∠AEB=90°,
∴∠CEA=180°-∠AEB=180°-90°=90°,
∵点D位AC中点,
∴DE=AD,
∴∠DAE=∠DEA,
∵OE=OA,
∴∠OEA=∠OAE,
∴∠OEA+∠DEA=∠OAE+∠DAE,
∴∠OED=∠BAC=90°,
∴DE⊥OE,
∴DE是⊙O的切线.
(2)解:∵∠BAC=90°,EF⊥AB,
∴AD∥EF,
∵DE∥AK,
∴四边形ADEG是平行四边形,
∵AD=ED,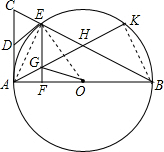
∴四边形ADEG是菱形,
∴AG=EG=2GF,
∴在Rt△AGF中,sin∠GAF=
=
,
∴∠GAF=30°,
∵DE∥AK,OE⊥DE,
∴AK⊥OE,
∴∠AOE=90°-30°=60°,
∵OE=OA,
∴△OEA是等边三角形,
∵点G在AK上,AK⊥OE,
∴EG=OG=2,
∴AG=EG=2,
∴AF=2×cos30°=
,
∴OA=2AF=2
,
∴AB=2OA=4
,
∴AK=4
×cos30°=6,BK=AB•sin30°=2
,
∴S△ABK=
AK•BK=6
.
∵AB是⊙O直径,
∴∠AEB=90°,
∴∠CEA=180°-∠AEB=180°-90°=90°,
∵点D位AC中点,
∴DE=AD,
∴∠DAE=∠DEA,
∵OE=OA,
∴∠OEA=∠OAE,
∴∠OEA+∠DEA=∠OAE+∠DAE,
∴∠OED=∠BAC=90°,
∴DE⊥OE,
∴DE是⊙O的切线.
(2)解:∵∠BAC=90°,EF⊥AB,
∴AD∥EF,
∵DE∥AK,
∴四边形ADEG是平行四边形,
∵AD=ED,

∴四边形ADEG是菱形,
∴AG=EG=2GF,
∴在Rt△AGF中,sin∠GAF=
| GF |
| AG |
| 1 |
| 2 |
∴∠GAF=30°,
∵DE∥AK,OE⊥DE,
∴AK⊥OE,
∴∠AOE=90°-30°=60°,
∵OE=OA,
∴△OEA是等边三角形,
∵点G在AK上,AK⊥OE,
∴EG=OG=2,
∴AG=EG=2,
∴AF=2×cos30°=
| 3 |
∴OA=2AF=2
| 3 |
∴AB=2OA=4
| 3 |
∴AK=4
| 3 |
| 3 |
∴S△ABK=
| 1 |
| 2 |
| 3 |
点评:此题考查了切线的性质、等边三角形的判定与性质、等腰三角形的性质以及三角函数等知识.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目
 如图,图中三角形是直角三角形,所有四边形是正方形,s1=9,s3=25,则s2是( )
如图,图中三角形是直角三角形,所有四边形是正方形,s1=9,s3=25,则s2是( )| A、4 | B、16 | C、144 | D、64 |
已知?ABCD.下列结论中,不正确的是( )
| A、当AB=BC时,它是菱形 |
| B、当AC⊥BD时,它是菱形 |
| C、当AC=BD时,它是正方形 |
| D、当∠ABC=90°时,它是矩形 |
 如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,BG平分∠ABC,EF∥BC,交AC于F,求证:AE=CF.
如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,BG平分∠ABC,EF∥BC,交AC于F,求证:AE=CF. 一个山坡的倾斜角为10°,坡上有一棵树AB,当阳光与水平线成50°角时,树影BC的长为6米,求树高AB.
一个山坡的倾斜角为10°,坡上有一棵树AB,当阳光与水平线成50°角时,树影BC的长为6米,求树高AB.