题目内容
 如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,BG平分∠ABC,EF∥BC,交AC于F,求证:AE=CF.
如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,BG平分∠ABC,EF∥BC,交AC于F,求证:AE=CF.考点:全等三角形的判定与性质,角平分线的性质
专题:证明题
分析:过E作EH∥CF交BC于H,可得四边形EHCF是平行四边形,则HE=CF,需证AE=HE,可通过证明△ABE≌△HBE(ASA)证得.
解答: 解:AE=CF.
解:AE=CF.
理由:过E作EH∥CF交BC于H,
∴∠3=∠C,
∵∠BAC=90°,AD⊥BC,
∴∠ABC+∠C=90°,∠ABD+∠BAD=90°,
∴∠C=∠BAD,
∴∠3=∠BAD,
在△ABE和△HBE中
,
∴△ABE≌△HBE(AAS),
∴AE=HE,
∵EF∥BC,EH∥CF,
∴四边形EHCF是平行四边形,
∴HE=CF,
∴AE=CF.
 解:AE=CF.
解:AE=CF.理由:过E作EH∥CF交BC于H,
∴∠3=∠C,
∵∠BAC=90°,AD⊥BC,
∴∠ABC+∠C=90°,∠ABD+∠BAD=90°,
∴∠C=∠BAD,
∴∠3=∠BAD,
在△ABE和△HBE中
|
∴△ABE≌△HBE(AAS),
∴AE=HE,
∵EF∥BC,EH∥CF,
∴四边形EHCF是平行四边形,
∴HE=CF,
∴AE=CF.
点评:此题主要考查平行四边形的判定和性质以及全等三角形的判定,熟练掌握性质定理和判定定理是解题的关键,平行四边形的五种判定方法与平行四边形的性质相呼应,每种方法都对应着一种性质,在应用时应注意它们的区别与联系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
计算(2a-3b)(2b+3a)的结果是( )
| A、4a2-9b2 |
| B、6a2-5ab-6b2 |
| C、6a2-5ab+6b2 |
| D、6a2-15ab+6b2 |
已知4×8m×16m=29,则m的值是( )
| A、1 | B、4 | C、3 | D、2 |
将函数y=x2-2x-5变形为y=a(x-h)2+k的形式,正确的是( )
| A、y=(x-1)2-5 |
| B、y=(x-2)2+5 |
| C、y=(x-1)2-6 |
| D、y=(x+1)2-4 |
 如图,△ABC中,AD平分∠BAC,∠1=∠2,求证:AB=AC.
如图,△ABC中,AD平分∠BAC,∠1=∠2,求证:AB=AC.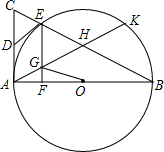 在Rt△ABC中,∠BAC=90°,以AB为直径⊙O交BC于点E,D为AC中点,EF⊥AB于点F.过A作AK∥DE交⊙O于K,交BC于H,交EF于G.
在Rt△ABC中,∠BAC=90°,以AB为直径⊙O交BC于点E,D为AC中点,EF⊥AB于点F.过A作AK∥DE交⊙O于K,交BC于H,交EF于G.