题目内容
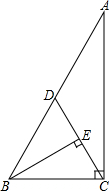 已知如图,在Rt△ABC中,∠ACB=90°,点D是斜边AB的中点,连接CD,BE⊥CD于点E.AB=10,S△ABC=24.
已知如图,在Rt△ABC中,∠ACB=90°,点D是斜边AB的中点,连接CD,BE⊥CD于点E.AB=10,S△ABC=24.(1)求AC的长度;
(2)求BE的长度;
(3)连接AE,求△ADE的面积S△ADE.
考点:勾股定理,直角三角形斜边上的中线
专题:
分析:(1)在直角三角形ABC中,设AC=x,利用勾股定理表示出BC,再利用面积法求出x的值,即可确定出AC的长;
(2)由直角三角形斜边上的中线等于斜边的一半求出CD的长,且三角形BCD与三角形ACD面积相等,利用三角形面积公式即可求出BE的长;
(3)连接AE,三角形AED与三角形ACE面积之比即为DE与CE之比,在直角三角形BDE中,利用勾股定理求出DE的长,进而求出CE的长,求出面积之比,即可确定出三角形ADE面积.
(2)由直角三角形斜边上的中线等于斜边的一半求出CD的长,且三角形BCD与三角形ACD面积相等,利用三角形面积公式即可求出BE的长;
(3)连接AE,三角形AED与三角形ACE面积之比即为DE与CE之比,在直角三角形BDE中,利用勾股定理求出DE的长,进而求出CE的长,求出面积之比,即可确定出三角形ADE面积.
解答: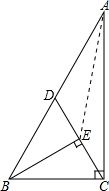 解:(1)在Rt△ABC中,∠ACB=90°,AB=10,
解:(1)在Rt△ABC中,∠ACB=90°,AB=10,
设AC=x,根据勾股定理得:BC=
,
∵S△ABC=
AC•BC=24,
∴
x
=24,
解得:x=6或x=8,
则AC=6或8;
(2)∵CD为Rt△ABC斜边AB上的中线,
∴CD=
AB=5,△BCD与△ACD面积相等,都为12,
∴
CD•BE=12,即5BE=24,
解得:BE=4.8;
(3)∵BD=AD=CD=5,BE=4.8,
∴在Rt△BDE中,根据勾股定理得:DE=
=1.6,
∴CE=5-1.6=3.4,即DE:CE=8:17,
∴S△ADE:S△ACE=8:17,
∵S△ADE+S△ACE=12,
∴S△ADE=
×12=
.
 解:(1)在Rt△ABC中,∠ACB=90°,AB=10,
解:(1)在Rt△ABC中,∠ACB=90°,AB=10,设AC=x,根据勾股定理得:BC=
| 100-x2 |
∵S△ABC=
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 100-x2 |
解得:x=6或x=8,
则AC=6或8;
(2)∵CD为Rt△ABC斜边AB上的中线,
∴CD=
| 1 |
| 2 |
∴
| 1 |
| 2 |
解得:BE=4.8;
(3)∵BD=AD=CD=5,BE=4.8,
∴在Rt△BDE中,根据勾股定理得:DE=
| 52-4.82 |
∴CE=5-1.6=3.4,即DE:CE=8:17,
∴S△ADE:S△ACE=8:17,
∵S△ADE+S△ACE=12,
∴S△ADE=
| 8 |
| 25 |
| 96 |
| 25 |
点评:此题考查了勾股定理,三角形面积求法,熟练掌握勾股定理是解本题的关键.

练习册系列答案
相关题目
 如图,△ABC的两条高BD、CE相交于点H,请问点A、E、H、D在同一个圆上吗?请说明理由.
如图,△ABC的两条高BD、CE相交于点H,请问点A、E、H、D在同一个圆上吗?请说明理由. 已知如图,在△ABC中,BD=CE,DF=EF,求证:AB=AC.
已知如图,在△ABC中,BD=CE,DF=EF,求证:AB=AC.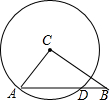 如图,在⊙C中,CA⊥CB,且CA=3,CB=4,求AD的长.
如图,在⊙C中,CA⊥CB,且CA=3,CB=4,求AD的长. 如图,已知在等边△ABC中,点D是边BC的中点,BF⊥AC于F点,连接DF并延长至E点,使得EF=DF,试判断△ACE的形状,并说明理由.
如图,已知在等边△ABC中,点D是边BC的中点,BF⊥AC于F点,连接DF并延长至E点,使得EF=DF,试判断△ACE的形状,并说明理由.