题目内容
13.写出一个一元二次方程,使它二次项系数为2,两根分别为2、-3,则该方程可以为2x2+2x-12=0.分析 设所求方程为ax2+bx+c=0,由二次项系数为2,可知a=2,由根与系数关系可知,-$\frac{b}{a}$=2+(-3),$\frac{c}{a}$=2×(-3),把a=2代入,分别求出b、c的值即可.
解答 解:设所求方程为ax2+bx+c=0.
∵二次项系数为2,
∴a=2.
∵方程的两根分别为2、-3,
∴-$\frac{b}{a}$=2+(-3)=-1,$\frac{c}{a}$=2×(-3)=-6,
解得:b=2,c=-12.
故所求方程为2x2+2x-12=0,
故答案为:2x2+2x-12=0.
点评 本题主要考查一元二次方程的根与系数的关系,比较简单.只要熟悉根与系数的关系,就很容易写出正确的结果.此外,本题还可以根据方程的根的定义,得出所求方程为2(x-2)(x+3)=0,再整理成一元二次方程的一般形式即可.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
2.矩形ABCD的面积是15,它的长与宽的比为3:1,则该矩形的宽为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
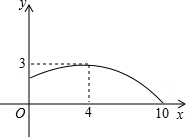 如图,一学生推铅球时,铅球行进高度y(m)与水平距离x(m)的函数图象为抛物线.
如图,一学生推铅球时,铅球行进高度y(m)与水平距离x(m)的函数图象为抛物线.