题目内容
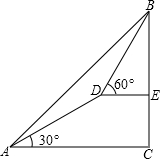一个人由山脚爬到山顶，须先爬倾斜角为30度的山坡300米到达D，再爬倾斜角为60度的山坡200米，求这座山的高度考点：解直角三角形的应用-坡度坡角问题
专题：
分析：在RT△ADF中，利用30°角和AD，求出DF即CE；在RT△BDE中，利用60°角和BD，求出BE；最后求CE和BE的和即可．
解答：
解：过D作DF⊥AC．
在Rt△ADF中，易得：CE=DF=AD×sin30°=150米，
在Rt△BDE中，易得：BE=BD×sin60°=100
米，
故山高BC=CE+BE=（150+100
）米．
故答案为：（150+100
）．
解：过D作DF⊥AC．在Rt△ADF中，易得：CE=DF=AD×sin30°=150米，
在Rt△BDE中，易得：BE=BD×sin60°=100
| 3 |
故山高BC=CE+BE=（150+100
| 3 |
故答案为：（150+100
| 3 |
点评：考查了解直角三角形的应用-坡度坡角问题，本题要求学生借助俯角关系构造直角三角形，并结合图形利用三角函数解直角三角形．
练习册系列答案
相关题目
某公司计划在一座圆锥形土丘上铺满草皮，土丘高50米，坡度i=1：
教室里的饮水机接通电源就进入自动程序，开机加热每分钟上升10℃，加热到100℃，停止加热，水温开始下降，此时水温（℃）与开机后用时（min）成反比例关系，直至水温降至30℃，饮水机关机．饮水机关机后即刻自动开机，重复上述自动程序．水温y（℃）和时间x（min）的关系如图．某天张老师在水温为30℃时，接通了电源，为了在上午课间时（8：45）能喝到不超过50℃的水，则接通电源的时间可以是当天上午的（ ）| A、7：50 | B、7：45 |
| C、7：30 | D、7：20 |
如图，A、B、C三点在⊙O上，且∠ABO=50°，则∠ACB等于（ ）| A、100° | B、80° |
| C、50° | D、40° |
圆锥底面圆的半径为2，母线长为8，则圆锥侧面展开图的圆心角是（ ）
| A、30° | B、40° |
| C、60° | D、90° |
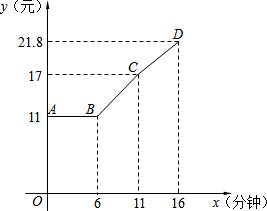某市出租车按里程计费标准为：不超过3公里部分，计费11元，超过3公里部分，按每公里2.4元计费．现在在此基础上，如果车速不超过12公里/小时，那么再加收0.48元/分钟，这项费用叫做“双计费”．图中三段折线表示某时间段内，一辆出租车的计费总额y（元）与行驶时间x（分钟）的函数关系（出租车在每段上均匀速行驶）．