题目内容
将正偶数按如表中的方式排成5列:
根据表中正偶数的排列规律,2014应在第 行,第 列.
| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | |
| 第1行 | 2 | 4 | 6 | 8 | |
| 第2行 | 16 | 14 | 12 | 10 | |
| 第3行 | 18 | 20 | 22 | 24 | |
| 第4行 | 32 | 30 | 28 | 26 | |
| … | … | … | … | … | … |
考点:规律型:数字的变化类
专题:
分析:观察各行各列的规律,首先分析两端的规律:第一列是偶数行,且数是16的
倍,第五列是奇数行有,且数是8的n倍.因为2014=16×125+2×7,2014=8×252-2.所以2014在第252行第2列.
| n |
| 2 |
解答:解:∵2014=16×125+2×7,2014=8×252-2,
∴可以看作是125×2行,再从251行数7个数,也可以看作252行再去掉2个数,也就是2014在第252行第2列.
故答案为:252,2.
∴可以看作是125×2行,再从251行数7个数,也可以看作252行再去掉2个数,也就是2014在第252行第2列.
故答案为:252,2.
点评:此题考查了规律型:图形的变化,首先注意分析两端中列的规律,然后分析出大概在第几行,再进一步推算所在的列.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
计算(-2a3b)2的结果是( )
| A、-2a6b |
| B、4a6b2 |
| C、-4a6b2 |
| D、4a5b2 |
把多项式x2-1分解因式为( )
| A、x+1 |
| B、x-1 |
| C、(x+1)(x-1) |
| D、(x+1)2 |
 如图,已知直线l⊥x轴于点D,点B(-1,y)为直线l上的动点,点C(x,0)为x轴上的动点,且-1<x<4,若点A(4,5),AC⊥BC,则y与x之间的函数关系式
如图,已知直线l⊥x轴于点D,点B(-1,y)为直线l上的动点,点C(x,0)为x轴上的动点,且-1<x<4,若点A(4,5),AC⊥BC,则y与x之间的函数关系式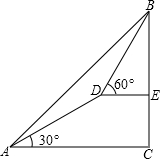 一个人由山脚爬到山顶,须先爬倾斜角为30度的山坡300米到达D,再爬倾斜角为60度的山坡200米,求这座山的高度
一个人由山脚爬到山顶,须先爬倾斜角为30度的山坡300米到达D,再爬倾斜角为60度的山坡200米,求这座山的高度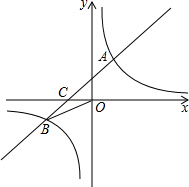 已知:如图,在平面直角坐标系中,一次函数y=ax+b (a≠0)的图象与反比例函数y=
已知:如图,在平面直角坐标系中,一次函数y=ax+b (a≠0)的图象与反比例函数y=