题目内容
在Rt△ABC中,∠ACB=90°,AC=
,cosA=
,如果将△ABC绕着点C旋转至△A′B′C的位置,使点B′落在∠ACB的角平分线上,A′B′与AC相交于点H,那么线段CH的长等于 .
| 2 |
| ||
| 2 |
考点:旋转的性质
专题:
分析:根据题意画出图形,进而利用旋转的性质以及锐角三角函数关系和等腰直角三角形求出三角形各边长,再利用三角形面积求出即可.
解答: 解:过点B′作B′F⊥AC于点F,A′D⊥AC于点D,
解:过点B′作B′F⊥AC于点F,A′D⊥AC于点D,
∵∠ACB=90°,点B′落在∠ACB的角平分线上,
∴∠BCB′=∠B′CA=ACA′=45°,
∴△CB′F,△CDA′都是等腰直角三角形,
∵AC=
,cosA=
,
∴
=
=
,
解得:AB=
,
∴BC=
,
∴B′C=
,
∴B′F=
×
=
,
A′D=
×CA′=1,
∴S△A′CB′=S△CHB′+S△CHA′=
×
×
=
×
×CH+
×1×CH,
解得:CH=
-1,
故答案为:
-1.
 解:过点B′作B′F⊥AC于点F,A′D⊥AC于点D,
解:过点B′作B′F⊥AC于点F,A′D⊥AC于点D,∵∠ACB=90°,点B′落在∠ACB的角平分线上,
∴∠BCB′=∠B′CA=ACA′=45°,
∴△CB′F,△CDA′都是等腰直角三角形,
∵AC=
| 2 |
| ||
| 2 |
∴
| AC |
| AB |
| ||
| AB |
| ||
| 2 |
解得:AB=
2
| ||
| 3 |
∴BC=
| ||
| 3 |
∴B′C=
| ||
| 3 |
∴B′F=
| ||
| 2 |
| ||
| 3 |
| ||
| 3 |
A′D=
| ||
| 2 |
∴S△A′CB′=S△CHB′+S△CHA′=
| 1 |
| 2 |
| ||
| 3 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
| 1 |
| 2 |
解得:CH=
| 3 |
故答案为:
| 3 |
点评:此题主要考查了旋转的性质以及锐角三角函数关系和三角形面积求法等知识,利用S△A′CB′=S△CHB′+S△CHA′求出是解题关键.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目

 如图,已知反比例函数y1=
如图,已知反比例函数y1=
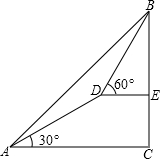 一个人由山脚爬到山顶,须先爬倾斜角为30度的山坡300米到达D,再爬倾斜角为60度的山坡200米,求这座山的高度
一个人由山脚爬到山顶,须先爬倾斜角为30度的山坡300米到达D,再爬倾斜角为60度的山坡200米,求这座山的高度