题目内容
14. 如图,△ABC为等边三角形,BD=CE,则∠AFE=60°.
如图,△ABC为等边三角形,BD=CE,则∠AFE=60°.
分析 由三角形ABC为等边三角形,根据等边三角形的性质可知三边相等,三内角都为60°,可得AB=CB,∠ABC=∠ACB=60°,又BD=CE,利用SAS的方法可得三角形ABD与三角形CEB全等;根据全等三角形的对应角相等可得∠DAB=∠EBC,又∠BFD=∠BAD+∠ABE=60°,最后利用对顶角相等求出∠AFE的度数.
解答 解:∵△ABC为等边三角形,
∴AB=BC=AC,∠ABC=∠ACB=60°,
在△ABD和△CEB中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABC=∠BCE}\\{BD=CE}\end{array}\right.$,
∴△ABD≌△CEB(SAS);
∴∠DAB=∠EBC,
又∵∠BFD=∠BAD+∠ABE=60°,
∴∠AFE=∠BFD=60°.
故答案为:60°.
点评 此题考查了全等三角形的判定与性质,等边三角形的性质,以及对顶角相等,利用了转化的思想,熟练掌握性质及定理是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.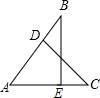 如图,AB=AC,∠AEB=∠ADC=90°,则判断△ABE≌△ACD的方法是( )
如图,AB=AC,∠AEB=∠ADC=90°,则判断△ABE≌△ACD的方法是( )
 如图,AB=AC,∠AEB=∠ADC=90°,则判断△ABE≌△ACD的方法是( )
如图,AB=AC,∠AEB=∠ADC=90°,则判断△ABE≌△ACD的方法是( )| A. | AAS | B. | HL | C. | SSS | D. | SAS |
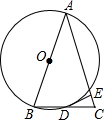 如图,△ABC的边AB为⊙O的直径,BC与⊙O交于点D,D为BC的中点,过点D作DE⊥AC于E.
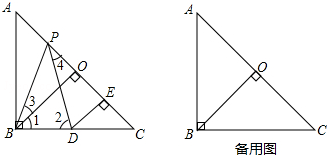
如图,△ABC的边AB为⊙O的直径,BC与⊙O交于点D,D为BC的中点,过点D作DE⊥AC于E.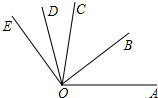 如图,OB是∠A0C的平分线,OD是∠COE的平分线.
如图,OB是∠A0C的平分线,OD是∠COE的平分线.