题目内容
2．一个密闭不透明的盒子里有若干个白球，在不允许将球倒出来的情况下，为估计白球的个数，小刚向其中放入8个黑球，黑球和白球除颜色外完全相同，摇匀后从中随机摸出一个球记下颜色，再把它放回盒中，不断重复，共摸球400次，其中80次摸到黑球，估计盒中大约有白球（ ）| A． | 32个 | B． | 36个 | C． | 38个 | D． | 40个 |
分析 可根据“黑球数量÷黑白球总数=黑球所占比例”来列等量关系式，其中“黑白球总数=黑球个数+白球个数“，“黑球所占比例=随机摸到的黑球次数÷总共摸球的次数”．
解答 解：设盒子里有白球x个，
根据$\frac{黑球的个数}{黑白球的总数}=\frac{摸到黑球的次数}{总摸球的次数}$得：
$\frac{8}{x+8}=\frac{80}{400}$，
解得：x=32．
经检验得x=32是方程的解．
故选A．
点评 考查了利用频率估计概率的知识，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系列出方程，再求解，注意分式方程要验根．
练习册系列答案
阅读快车系列答案
相关题目
12．
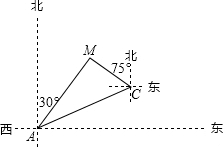如图，某天然气公司的主输气管道从A市的北偏东60°方向直线延伸，测绘员在A处测得要安装天然气的M小区在A市的北偏东30°方向，测绘员沿主输气管道步行1000米到达点C处，测得M小区位于点C的北偏西75°方向，试在主输气管道上寻找支管道连接点N，使到该小区铺设的管道最短，此时AN的长约是（ ）$\sqrt{2}≈{1.4^{\;}}{，^{\;}}\sqrt{3}≈1.7$．
如图，某天然气公司的主输气管道从A市的北偏东60°方向直线延伸，测绘员在A处测得要安装天然气的M小区在A市的北偏东30°方向，测绘员沿主输气管道步行1000米到达点C处，测得M小区位于点C的北偏西75°方向，试在主输气管道上寻找支管道连接点N，使到该小区铺设的管道最短，此时AN的长约是（ ）$\sqrt{2}≈{1.4^{\;}}{，^{\;}}\sqrt{3}≈1.7$．| A． | 350米 | B． | 650米 | C． | 634米 | D． | 700米 |
13．一个由四舍五入得到的近似数为2.30，则原来的数可能是（ ）
| A． | 2.34 | B． | 2.29 | C． | 2.3049 | D． | 2.2949 |
10．如图，在直角坐标系中，已知点A（-3，0）、B（0，4），对△OAB连续作旋转变换，依次得到△1、△2、△3、△4、…，△16的直角顶点的坐标为（ ）
| A． | （60，0） | B． | （72，0） | C． | （67$\frac{1}{5}$，$\frac{9}{5}$） | D． | （79$\frac{1}{5}$，$\frac{9}{5}$） |
如图，△ABC为等边三角形，BD=CE，则∠AFE=60°．