题目内容
19.如图,已知在Rt△ABC中,AB=BC,∠ABC=90°,BO⊥AC于点O,点P是射线AC上一动点,点D是射线BC上一动点,PB=PD.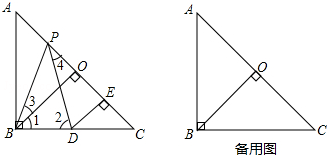
(1)如图1,当点P在线段OA上,DE⊥AC于点E.,求证:△BPO≌△PDE.
(2)特殊位置,证明结论
当PB平分∠ABO,其余条件不变.试探究线段CD和AP的数量关系,并加以证明.
(3)拓展应用,探索新知
当点P在射线OC上运动时时,其余条件不变.若OP=nCP时,请直接写出CD与AP的数量关系.(不必写解答过程)
分析 (1)求出∠3=∠4,∠BOP=∠PED=90°,根据AAS证△BPO≌△PDE即可;
(2)求出∠ABP=∠4,求出△ABP≌△CPD,即可得出答案;
(3)分当点P在线段OC上和点P在线段OC延长线上两种情况解答即可.
解答 (1)证明:∵PB=PD,
∴∠2=∠PBD,
∵AB=BC,∠ABC=90°,
∴∠C=45°,
∵BO⊥AC,
∴∠1=45°,
∴∠1=∠C=45°,
∵∠3=∠PBO-∠1,∠4=∠2-∠C,
∴∠3=∠4,
∵BO⊥AC,DE⊥AC,
∴∠BOP=∠PED=90°,
在△BPO和△PDE中,
∵$\left\{\begin{array}{l}{∠3=∠4}\\{∠BOP=∠PED}\\{BP=PD}\end{array}\right.$,
∴△BPO≌△PDE(AAS);
(2)CD=AP,理由如下:
由(1)可得:∠3=∠4,
∵BP平分∠ABO,
∴∠ABP=∠3,
∴∠ABP=∠4,
在△ABP和△CPD中,
∵$\left\{\begin{array}{l}{∠A=∠C}\\{∠ABP=∠4}\\{PB=CD}\end{array}\right.$,
∴△ABP≌△CPD(AAS),
∴AP=CD.
(3)当点P在线段OC上时,CD=$\frac{\sqrt{2}n}{2n+1}$AP;
当点P在线段OC延长线上时,CD=$\frac{\sqrt{2}n}{2n-1}$AP.
点评 本题考查了全等三角形的性质和判定,等腰直角三角形性质,等腰三角形性质等知识点的综合应用,主要考查学生的推理和计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.如图,在直角坐标系中,已知点A(-3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4、…,△16的直角顶点的坐标为( )


| A. | (60,0) | B. | (72,0) | C. | (67$\frac{1}{5}$,$\frac{9}{5}$) | D. | (79$\frac{1}{5}$,$\frac{9}{5}$) |
4.小敏到距家1500米的学校去上学,小敏出发10分钟后,小敏的爸爸立即去追小敏,且在距离学校60米的地方追上了她.已知爸爸比小敏的速度快100米/分,求小敏的速度.若设小敏的速度为x米/分,则根据题意所列方程正确的是( )
| A. | $\frac{1440}{x}=\frac{1440}{x+100}+10$ | B. | $\frac{1440}{x-100}-\frac{1440}{x}=10$ | ||
| C. | $\frac{1440}{x}=\frac{1440}{x-100}+10$ | D. | $\frac{1440}{x+100}-\frac{1440}{x}=10$ |
 如图,△ABC为等边三角形,BD=CE,则∠AFE=60°.
如图,△ABC为等边三角形,BD=CE,则∠AFE=60°. 如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连结DE.
如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连结DE. 如图所示,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=15,则△PCD的周长为30.
如图所示,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=15,则△PCD的周长为30.