题目内容
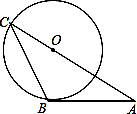
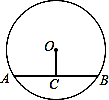
如图,AB是⊙O的切线,B为切点,AO的延长线交⊙O于C点,连接BC,若∠A=30°,AB=2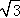 ,则AC等于( )
,则AC等于( )
A.4 B.6 C.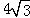 D.
D.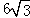
B【考点】切线的性质.
【分析】连接OB,则△AOB是直角三角形,利用三角函数即可求得OA的长,则AC即可求解.
【解答】解:连接OB.
∵AB是⊙O的切线,B为切点,
∴OB⊥AB,
在直角△OAB中,OB=AB•tanA=2 ×
×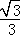 =2,
=2,
则OA=2OB=4,
∴AC=4+2=6.
故选B.
【点评】本题考查了三角函数以及切线的性质,正确判断△OAB是直角三角形是关键.

练习册系列答案
相关题目


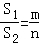 ,
, =
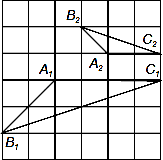
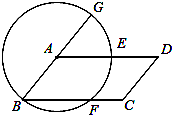
=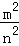 ,根据上述条件,判断S1+S3与S2+S4的大小关系,并说明理由.
,根据上述条件,判断S1+S3与S2+S4的大小关系,并说明理由.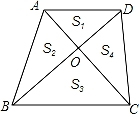
 是完成平方公式,那么k的值是
是完成平方公式,那么k的值是 B.
B. C.
C. D.
D.
 区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.
区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.