题目内容
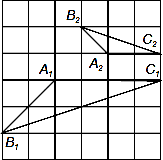
学习相似三角形和解直角三角形的相关内容后,张老师请同学们交流这样的一个问题:“如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形是否相似?”.那么你认为△A1B1C1和△A2B2C2 .(填相似或不相似);理由是 .
 =
= =
= .
.
【考点】相似三角形的判定.
【专题】网格型.
【分析】由勾股定理求出A1B1=2 ,B1C1=2
,B1C1=2 ,A2B2=
,A2B2= ,B2C2=
,B2C2= ,证出
,证出 =
= =
= =2,由三边成比例的两个三角形相似即可得出结论.
=2,由三边成比例的两个三角形相似即可得出结论.
【解答】解:由题意得:A1C1=4,A2C2=2,
由勾股定理得:A1B1= =2
=2 ,B1C1=
,B1C1= =2
=2 ,
,
A2B2= =
= ,B2C2=
,B2C2= =
= ,
,
∴ =
= =2,
=2, =
= =2,
=2, =
= =2,
=2,
∴ =
= =
= =2,
=2,
∴△A1B1C1∽△A2B2C2.
故答案为:相似, =
= =
= .
.
【点评】本题考查了相似三角形的判定方法、勾股定理;熟练掌握勾股定理,熟记三边成比例的两个三角形相似是解决问题的关键.

练习册系列答案
相关题目
 (2)将抛物线沿x轴翻折,得到图象G,
(2)将抛物线沿x轴翻折,得到图象G, B.
B. C.
C. D.1
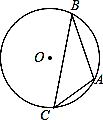
D.1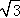 ,则AC等于( )
,则AC等于( )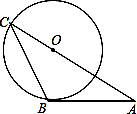
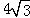 D.
D.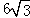
 .
. 的顶点坐标是( )
的顶点坐标是( )