题目内容
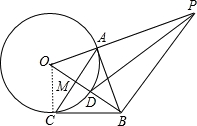
.如图,点A是⊙O上一点,OA⊥AB,且OA=1,AB= ,OB交⊙O于点D,作AC⊥OB,垂足为M,并交⊙O于点C,连接BC.
,OB交⊙O于点D,作AC⊥OB,垂足为M,并交⊙O于点C,连接BC.
(1)求证:BC是⊙O的切线;
(2)过点B作BP⊥OB,交OA的延长线于点P,连接PD,求sin∠BPD的值.

【考点】切线的判定;全等三角形的判定与性质;勾股定理;垂径定理.
【专题】证明题.
【分析】(1)连结OC,根据垂径定理由AC⊥OB得AM=CM,于是可判断OB为线段AC的垂直平分线,所以BA=BC,然后利用“SSS”证明△OAB≌△OCB,得到∠OAB=∠OCB,由于∠OAB=90°,则∠OCB=90°,于是可根据切线的判定定理得BC是⊙O的切线;
(2)在Rt△OAB中,根据勾股定理计算出OB=2,根据含30度的直角三角形三边的关系得∠ABO=30°,∠AOB=60°,在Rt△PBO中,由∠BPO=30°得到PB=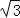 OB=2
OB=2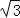 ;在Rt△PBD中,BD=OB﹣OD=1,根据勾股定理计算出PD=
;在Rt△PBD中,BD=OB﹣OD=1,根据勾股定理计算出PD=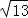 ,然后利用正弦的定义求sin∠BPD的值.
,然后利用正弦的定义求sin∠BPD的值.
【解答】(1)证明:连结OC,如图,
∵AC⊥OB,
∴AM=CM,
∴OB为线段AC的垂直平分线,
∴BA=BC,
在△OAB和△OCB中
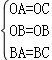 ,
,
∴△OAB≌△OCB(SSS),
∴∠OAB=∠OCB,
∵OA⊥AB,
∴∠OAB=90°,
∴∠OCB=90°,
∴OC⊥BC,
故BC是⊙O的切线;
(2)解:在Rt△OAB中,OA=1,AB=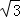 ,
,
∴OB=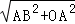 =2,
=2,
∴∠ABO=30°,∠AOB=60°,
∵PB⊥OB,
∴∠PBO=90°,∠BPO=30°,
在Rt△PBO中,OB=2,
∴PB=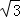 OB=2
OB=2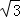 ,
,
在Rt△PBD中,BD=OB﹣OD=2﹣1=1,PB=2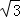 ,
,
∴PD=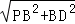 =
=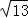 ,
,
∴sin∠BPD= =
=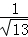 =
= .
.
【点评】本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了垂径定理、勾股定理和全等三角形的判定与性质.

 阅读快车系列答案
阅读快车系列答案学校李老师布置了两道解方程的作业题:
选用合适的方法解方程:
(1)x(x+1)=2x;(2)(x+1)(x﹣3)=7
以下是王萌同学的作业:
| 解:(1)移项,得x(x+1)﹣2x=0 分解因式得,x(x+1﹣2)=0 所以,x=0,或x﹣1=0 所以,x1=0,x2=1 | (2)变形得,(x+1)(x﹣3)=1×7 所以,x+1=7,x﹣3=1 解得,x1=6,x2=4 |
请你帮王萌检查他的作业是否正确,把不正确的改正过来.

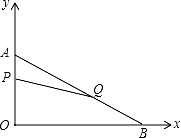
 的图象在第二、第四象限内,函数图象上有两点A(2
的图象在第二、第四象限内,函数图象上有两点A(2 ,y1)、B(5,y2),则y1与y2的大小关系是__________.
,y1)、B(5,y2),则y1与y2的大小关系是__________.
 图象的每条曲线上,y都随x的增大而增大,则k的取值范围是( )
图象的每条曲线上,y都随x的增大而增大,则k的取值范围是( ) +|b﹣4|=0,求该直角三角形的斜边长.
+|b﹣4|=0,求该直角三角形的斜边长.