Question

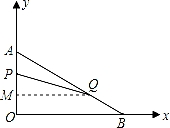
在平面直角坐标系内，已知点A（0，6），点B（8，0），动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动，同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动，设点P、Q移动的时间为t秒．

（1）求直线AB的解析式；

（2）当t=2秒时，求四边形OPQB的面积；

（3）当t为何值时，以点A、P、Q为顶点的三角形与△AOB相似？

　

Answer 1

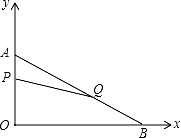
【考点】一次函数综合题．

【分析】（1）根据直线经过点A、B，利用待定系数法求出函数的解析式；

（2）过点Q作QM⊥OA于M，由△AMQ∽△AOB求出QM的值，求出四边形OPQB的面积；

（3）以点A、P、Q为顶点的三角形与△AOB相似，分△APQ∽△AOB和△AQP∽△AOB两种情况讨论，根据相似三角形的对应边的比相等，就可以求出t的值．

【解答】解：（1）设直线AB的解析式为y=kx+b，

将点A（0，6）、点B（8，0）代入得，

，

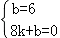解得，，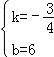

∴直线AB的解析式为y=﹣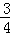x+6；

（2）过点Q作QM⊥OA于M，

当t=2秒时，AP=2，AQ=AB﹣BQ=6，

在Rt△OAB中，OA=6，OB=8，

由勾股定理可得，AB=10，

∵∠AOB=90°，QM⊥OA，

∴△AMQ∽△AOB，

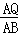∴=，即=，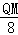

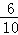解得，QM=，

∴△APQ的面积=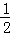×AP×QM=，

∴四边形OPQB的面积=△AOB的面积﹣△APQ的面积=；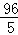

（3）由题意得，AO=6，BO=8，AB=10，AP=t，AQ=10﹣2t，

当△APQ∽△AOB时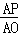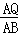， =，即=，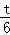

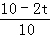解得，t=；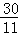

当△APQ∽△ABO时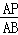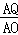， =，即=，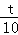

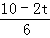解得，t=，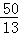

因此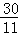，t=或t=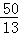时，以点A．P．Q为顶点的三角形与△AOB相似．

【点评】本题考查的是相似三角形的判定和性质以及一次函数解析式的确定，掌握相似三角形的判定定理和性质定理、待定系数法求一次函数解析式是解题的关键．