题目内容
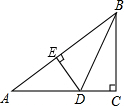 如图,在直角三角形ABC中,∠C=90°,BC=6cm,AC=8cm,按图中方法将△BCD沿BD折叠,使点C落在AB边的E点,那么△ADE的面积是
如图,在直角三角形ABC中,∠C=90°,BC=6cm,AC=8cm,按图中方法将△BCD沿BD折叠,使点C落在AB边的E点,那么△ADE的面积是考点:翻折变换(折叠问题)
专题:
分析:根据勾股定理得到AB=
,根据折叠的性质得到DC=DE,BC=BE=6cm,则AE=4cm,在Rt△ADE中利用勾股定理得(8-x)2=x2+42,解得x=3,然后根据三角形的面积公式计算即可.
| AC2+BC2 |
解答:解:∵∠C=90°,BC=6cm,AC=8cm,
∴AB=
=10(cm);
∵将△BCD沿BD折叠,使点C落在AB边的E点,
∴△BCD≌△BED,
∴∠C=∠BED=90°,DC=DE,BC=BE=6cm,
∴AE=AB-BE=4cm,
设DC=xcm,则AD=(8-x)cm,
在Rt△ADE中,AD2=AE2+ED2,
即(8-x)2=x2+42,解得x=3,
∵∠AED=90°,
∴△ADE的面积=
×AE×ED=
×4×3=6(cm2).
故答案为:6cm2.
∴AB=
| 82+62 |
∵将△BCD沿BD折叠,使点C落在AB边的E点,
∴△BCD≌△BED,
∴∠C=∠BED=90°,DC=DE,BC=BE=6cm,
∴AE=AB-BE=4cm,
设DC=xcm,则AD=(8-x)cm,
在Rt△ADE中,AD2=AE2+ED2,
即(8-x)2=x2+42,解得x=3,
∵∠AED=90°,
∴△ADE的面积=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:6cm2.
点评:本题考查了折叠的性质以及勾股定理等知识,利用折叠性质折叠前后两图形全等,即对应角相等,对应线段相等,对应点的连线段被折痕垂直平分是解题关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
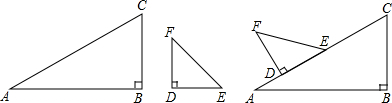
 如图,点A(a,1)、B(-1,b)都在双曲线y=-
如图,点A(a,1)、B(-1,b)都在双曲线y=-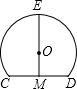 如图,M是CD中点,EM⊥CD,若CD=6,EM=9,则C、E、D三点的所在圆的半径为
如图,M是CD中点,EM⊥CD,若CD=6,EM=9,则C、E、D三点的所在圆的半径为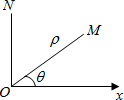 在平面内取一个定点O,叫极点,引一条射线Ox,叫做极轴,再选定一个长度单位和角度的正方向(通常取逆时针方向).对于平面内任何一点M,用ρ表示线段OM的长度,θ表示从Ox到OM的角度,ρ叫做点M的极径,θ叫做点M的极角,有序数对(ρ,θ)就叫点M的极坐标,若ON⊥OX,且点N到极点O的距离为4个单位长度,则点N的极坐标可表示为
在平面内取一个定点O,叫极点,引一条射线Ox,叫做极轴,再选定一个长度单位和角度的正方向(通常取逆时针方向).对于平面内任何一点M,用ρ表示线段OM的长度,θ表示从Ox到OM的角度,ρ叫做点M的极径,θ叫做点M的极角,有序数对(ρ,θ)就叫点M的极坐标,若ON⊥OX,且点N到极点O的距离为4个单位长度,则点N的极坐标可表示为 如图,△ACB和△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上,若
如图,△ACB和△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上,若