如图.沿矩形ABCD的对角线折叠.先折出折痕AC.再折叠AB.使AB落在对角线AC上.折痕AE.若AD=8.AB=6．则BE=3．题目和参考答案——青夏教育精英家教网—

题目内容

5．

如图，沿矩形ABCD的对角线折叠，先折出折痕AC，再折叠AB，使AB落在对角线AC上，折痕AE，若AD=8，AB=6．则BE=3．

分析如答图所示AB沿AE折叠后点B的对应点为F．利用勾股定理列式求出AC，设BE=x，表示出CE，根据翻折的性质可得BE=EF，AF=AB，再求出CF，然后利用勾股定理列方程求出x即可．

解答解：如图所示：AB沿AE折叠后点B的对应点为F．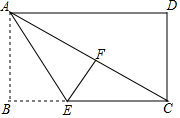

由勾股定理得，AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10．
设BE=x，则CE=8-x．
由翻折的性质得：BE=EF=x，AF=AB=6，
所以CF=10-6=4．
在Rt△CEF中，由勾股定理得，EF²+CF²=CE²，即x²+4²=（8-x）²，
解得x=3，即BE=3．
故答案为：3．

点评本题考查了翻折变换的性质，勾股定理，此类题目，熟记性质并利用勾股定理列出方程是解题的关键．

练习册系列答案

16．△ABC中，∠C=90°，CD⊥AB于D，则sinB=（　　）

	A．	平行四边形的两组对边分别相等
	B．	矩形的对角线相等
	C．	两组对边分别相等四边形是平行四边形
	D．	对角线相等的四边形是矩形

10．把边长为1的正方形纸片OABC放在直线m上，OA边在直线m上，然后将正方形纸片绕着顶点A按顺时针方向旋转90°，此时，点O运动到了点O₁处（即点B处），点C运动到了点C₁处，点B运动到了点B₁处，又将正方形纸片AO₁C₁B₁绕B₁点，按顺时针方向旋转90°…，按上述方法经过61次旋转后，顶点O经过的总路程为$\frac{15\sqrt{2}+31}{2}$π．

17．探索与研究
知识链接：
已知，点D是△ABC外接圆上的一点（不与点A、B重合）．D₁、D₂为平面内任意点．
①如图①，当点C与D、D₁、D₂在直线AB同侧时，在边AB所对的∠D、∠D₁、∠D₂三个角中，唯有∠D=∠C．
②如图②，当点C与D、D₁、D₂在直线AB两侧时，在边AB所对的∠D、∠D₁、∠D₂三个角中，唯有∠D与∠C互补．
逆向思维：
已知，⊙O是△ABC的外接圆，若△ABC的某边所对的∠D与△ABC该边所对的内角相等或互补，则点D在该三角形的外接圆上．（注：该结论在解答以下题目时可直接使用，无需证明）
迁移应用：
（1）如图③，四边形ABCD中∠ACB=60°，请用直尺和圆规在四边形ABCD的边上确定点E的位置（不写作法，保留作图痕迹），使∠AEB=60°．若有不同的位置，请用E₁、E₂…区分．
（2）如图④，AB=AD，AE∥BD，∠ECA=∠CDB，求证：点D在△ACE的外接圆上．
（3）如图⑤，在平面直角坐标系中，抛物线y=-ax²+3ax+4a（a＞0，a为常数）的图象与y轴交于点C，交x轴于点A、B（A点在B点左侧），顶点为D．抛物线的对称轴上是否存在点P，使∠BPC=∠BAC？若存在，求出点P的坐标（可用a的代数式表示），若不存在，请说明理由．

14．下列图形中，不是中心对称图形的是（　　）

15．运用乘法公式计算：
（1）（x-2y+3z）²；
（2）（2a+b+1）（2a-b-1）

试题分类