题目内容
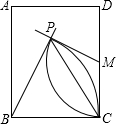 如图,长方形ABCD中,M为CD中点,以点B、M为圆心,分别以BC长、MC长为半径画弧,两弧相交于点P.若∠PMC=110°,则∠BPC的度数为
如图,长方形ABCD中,M为CD中点,以点B、M为圆心,分别以BC长、MC长为半径画弧,两弧相交于点P.若∠PMC=110°,则∠BPC的度数为考点:矩形的性质,等腰三角形的性质
专题:
分析:根据三角形内角和定理和等腰三角形两底角相等求出∠MCP,然后求出∠BCP,再根据等腰三角形两底角相等和三角形内角和定理求解即可.
解答:解:∵以B、M为圆心,分别以BC长、MC长为半径的两弧相交于P点,
∴BP=BC,MP=MC,
∵∠PMC=110°,
∴∠MCP=
(180°-∠PMC)=
(180°-110°)=35°,
在长方形ABCD中,∠BCD=90°,
∴∠BCP=90°-∠MCP=90°-35°=55°,
∴∠BCP=∠BPC=55°.
故答案为:55°.
∴BP=BC,MP=MC,
∵∠PMC=110°,
∴∠MCP=
| 1 |
| 2 |
| 1 |
| 2 |
在长方形ABCD中,∠BCD=90°,
∴∠BCP=90°-∠MCP=90°-35°=55°,
∴∠BCP=∠BPC=55°.
故答案为:55°.
点评:本题考查了矩形的四个角都是直角的性质,等腰三角形两底角相等的性质以及等边对等角,三角形内角和等于180°的知识点.

练习册系列答案
相关题目
 如图,四边形ABCD是矩形,把矩形沿直线BD折叠,点C落在点E处,连接BE,与AD交于点M.
如图,四边形ABCD是矩形,把矩形沿直线BD折叠,点C落在点E处,连接BE,与AD交于点M.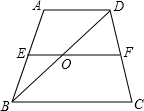 如图,在梯形ABCD中,AD∥BC,点E在AB上,点F在CD上,EF为中位线,EF与BD交于点O,若FO-EO=5,则BC-AD=
如图,在梯形ABCD中,AD∥BC,点E在AB上,点F在CD上,EF为中位线,EF与BD交于点O,若FO-EO=5,则BC-AD= 如图,△ABC中,D为边AC的中点,设BD=
如图,△ABC中,D为边AC的中点,设BD= 如图,边长为2的正方形ABCD绕点A逆时针旋转45度后得到正方形AB′C′D′,则在旋转过程中点D到D′的路径长是
如图,边长为2的正方形ABCD绕点A逆时针旋转45度后得到正方形AB′C′D′,则在旋转过程中点D到D′的路径长是 调查机构对某地区1000名20~30岁年龄段观众周五综艺节目的收视选择进行了调查,相关统计图如下,请根据图中信息,估计该地区20000名20~30岁年龄段观众选择观看《最强大脑》的人数约为
调查机构对某地区1000名20~30岁年龄段观众周五综艺节目的收视选择进行了调查,相关统计图如下,请根据图中信息,估计该地区20000名20~30岁年龄段观众选择观看《最强大脑》的人数约为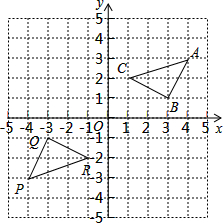 如图,三角形PQR是三角形ABC经过某种变换后得到的图形,分别写出点A与点P,点B与点Q,点C与点R的坐标,并观察它们之间的关系,如果三角形ABC中任意一点M的坐标为(a,b),那么它的对应点N的坐标是什么?
如图,三角形PQR是三角形ABC经过某种变换后得到的图形,分别写出点A与点P,点B与点Q,点C与点R的坐标,并观察它们之间的关系,如果三角形ABC中任意一点M的坐标为(a,b),那么它的对应点N的坐标是什么?