题目内容
18.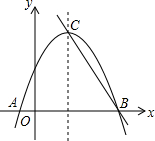 如图,抛物线y=-$\frac{4}{9}$x2+$\frac{16}{9}$x+$\frac{20}{9}$与x轴相交于A、B两点,抛物线的顶点为C,问:在抛物线的对称轴上是否存在一点P,使⊙P与x轴和直线BC都相切?若存在,请求出P的坐标;若不存在,请说明理由.
如图,抛物线y=-$\frac{4}{9}$x2+$\frac{16}{9}$x+$\frac{20}{9}$与x轴相交于A、B两点,抛物线的顶点为C,问:在抛物线的对称轴上是否存在一点P,使⊙P与x轴和直线BC都相切?若存在,请求出P的坐标;若不存在,请说明理由.
分析 首先求出点A和点B的坐标,进而求出抛物线的顶点坐标以及对称轴,然后作出图形,利用勾股定理的知识求出点P的纵坐标即可.
解答 解:令y=-$\frac{4}{9}$x2+$\frac{16}{9}$x+$\frac{20}{9}$=0,
即-4x2+16x+20=0,
∴x2-4x-5=0,
∴(x-5)(x+1)=0,
∴x1=-1,x2=5,
∴点A(-1,0),点B(5,0),
∴抛物线对称轴为x=2,顶点坐标为(2,4),
假设存在点P,使⊙P与x轴和直线BC都相切,
则点P是∠ABC的角平分线与对称轴的交点,如图,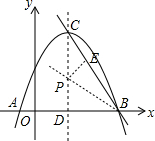
过P点作PE⊥BC于点E,
则PE=PD,BD=BE,
∵CD=4,BC=3,
∴BC=5,
设PD=PE=x,
则PC=4-x,CE=2,
∴CE2+PE2=PC2,
∴22+x2=(4-x)2,
∴x=$\frac{3}{2}$,
∴P点坐标为(2,$\frac{3}{2}$),
即抛物线的对称轴上存在一点P,使⊙P与x轴和直线BC都相切.
点评 本题主要考查了抛物线与x轴交点问题,解答本题的关键是找出点P在∠ABC的角平分线与对称轴的交点上,此题难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.在 0,-(-2),-|-3|,(-4)2,-52这些数中,属于负数的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
6.在△ABC中,∠A=20°,∠B=60°,则∠C的度数( )
| A. | 80° | B. | 90° | C. | 20° | D. | 100° |
7.乘雪橇沿倾斜角是30°的斜坡滑下,滑下的路程S(米)与时间t(秒)间的关系式为S=10t+t2,若滑到坡底的时间为2秒,则此人下滑的高度为( )
| A. | 24米 | B. | 12米 | C. | 12$\sqrt{3}$米 | D. | 6米 |
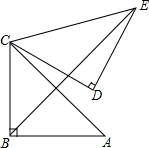 如图,在Rt△ABC中,∠ABC=90°,AB=BC=$\sqrt{2}$,将△ABC绕点C逆时针旋转60°,得到△CDE,连结BE,求BE的长.
如图,在Rt△ABC中,∠ABC=90°,AB=BC=$\sqrt{2}$,将△ABC绕点C逆时针旋转60°,得到△CDE,连结BE,求BE的长.