题目内容
9.(1)解不等式$\frac{x-1}{2}≤1+x$,(2)解不等式组$\left\{\begin{array}{l}3x+1>4\\ 4-2x≥0\end{array}\right.$并把解集表示在数轴上

(3)分解因式:2xy2-18x
(4)分解因式:(a2+1)2-4a2
(5)用简便方法计算:5.652-4.352.
分析 (1)不等式去分母,移项合并,把x系数化为1,即可求出解集;
(2)分别求出不等式组中两不等式的解集,找出两解集的公共部分确定出解集,表示在数轴上即可;
(3)原式提取公因式,再利用平方差公式分解即可;
(4)原式利用平方差公式及完全平方公式分解即可;
(5)原式利用平方差公式变形,计算即可得到结果.
解答 解:(1)去分母得:x-1≤2+2x,
解得:x≥-3;
(2)不等式解得:1<x≤2,
(3)原式=2x(y2-9)=2x(y+3)(y-3);
(4)原式=(a2+1+2a)(a2+1-2a)=(a+1)2(a-1)2;
(5)原式=(5.65+4.35)×(5.65-4.35)=10×1.3=13.
点评 此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
相关题目
19.在△ABC中,a、b、c是它的三条边,则下列条件不能判定其为直角三角形的是( )
| A. | ∠B=∠A+∠C | B. | a2-b2=c2 | C. | ∠A:∠B:∠C=5:4:3 | D. | a:b:c=5:12:13 |
20.下列式子计算正确的是( )
| A. | (-1)-1=1 | B. | (π-3.14)0=0 | C. | 24÷26=22 | D. | ${({-\frac{1}{2}})^{-3}}$=-8 |
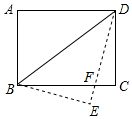 如图,在矩形ABCD中,AB=6,BC=8,将矩形纸片沿BD折叠,使点A落在点E处,设DE与BC相交于点F,则BF的长为$\frac{25}{4}$.
如图,在矩形ABCD中,AB=6,BC=8,将矩形纸片沿BD折叠,使点A落在点E处,设DE与BC相交于点F,则BF的长为$\frac{25}{4}$. 如图,正方形ABCD的边长为2,点E是BC边上的一动点,点F是CD上一点,且CE=DF,AF、DE相交于点O,BO=BA,则OC的值为$\frac{2}{5}$$\sqrt{10}$.
如图,正方形ABCD的边长为2,点E是BC边上的一动点,点F是CD上一点,且CE=DF,AF、DE相交于点O,BO=BA,则OC的值为$\frac{2}{5}$$\sqrt{10}$.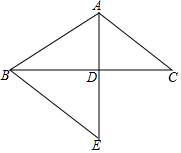 如图,△ABC中,AB=AC,线段BC的垂直平分线AD交BC于点D,过点BE作BE∥AC,交AD的延长线于点E,求证:AB=BE.
如图,△ABC中,AB=AC,线段BC的垂直平分线AD交BC于点D,过点BE作BE∥AC,交AD的延长线于点E,求证:AB=BE.