题目内容
19.在△ABC中,a、b、c是它的三条边,则下列条件不能判定其为直角三角形的是( )| A. | ∠B=∠A+∠C | B. | a2-b2=c2 | C. | ∠A:∠B:∠C=5:4:3 | D. | a:b:c=5:12:13 |
分析 由三角形内角和定理及勾股定理的逆定理进行判断即可.
解答 解:A、∠B=∠A+∠C,又∠A+∠B+∠C=180°,则∠B=90°,是直角三角形;
B、由a2-b2=c2,得c2+b2=a2,符合勾股定理的逆定理,是直角三角形;
C、∠A:∠B:∠C=5:4:3,又∠A+∠B+∠C=180°,则∠A=180°×$\frac{5}{12}$=75°,不是直角三角形;
D、∵a:b:c=5:12:13,
设a=5k,b=12k,c=13k,
由a2+b2=25k2+144k2=169k2=c2,符合勾股定理的逆定理,是直角三角形.
故选C.
点评 本题考查了直角三角形的判定,注意在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.

练习册系列答案
相关题目
9. 如图,小华同学在距离某建筑物6米的点A处测得广告牌B点、C点的仰角分别为52°和35°,则广告牌的高度BC约为( )(精确到0.1米)(sin35°=0.57,cos35°=0.82,tan35°=0.70;sin52°=0.79,cos52°=0.62,tan52°=1.28)
如图,小华同学在距离某建筑物6米的点A处测得广告牌B点、C点的仰角分别为52°和35°,则广告牌的高度BC约为( )(精确到0.1米)(sin35°=0.57,cos35°=0.82,tan35°=0.70;sin52°=0.79,cos52°=0.62,tan52°=1.28)
 如图,小华同学在距离某建筑物6米的点A处测得广告牌B点、C点的仰角分别为52°和35°,则广告牌的高度BC约为( )(精确到0.1米)(sin35°=0.57,cos35°=0.82,tan35°=0.70;sin52°=0.79,cos52°=0.62,tan52°=1.28)
如图,小华同学在距离某建筑物6米的点A处测得广告牌B点、C点的仰角分别为52°和35°,则广告牌的高度BC约为( )(精确到0.1米)(sin35°=0.57,cos35°=0.82,tan35°=0.70;sin52°=0.79,cos52°=0.62,tan52°=1.28)| A. | 3.4米 | B. | 3.5米 | C. | 9.7米 | D. | 5.5米 |
11. 如图所示的几何体的主视图是( )
如图所示的几何体的主视图是( )
 如图所示的几何体的主视图是( )
如图所示的几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
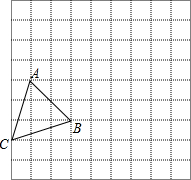 如图,将方格纸中的△ABC先向右平移6个单位长度,再向上平移4个单位,得到△A1B1C1.
如图,将方格纸中的△ABC先向右平移6个单位长度,再向上平移4个单位,得到△A1B1C1.