题目内容
在Rt△ABC中，∠ACB=90°，若sinB=
，则tanA=（ ）
| 5 |
| 13 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：互余两角三角函数的关系
专题：几何图形问题
分析：根据题意做出图形，然后利用三角函数的定义及勾股定理求解．
解答：
解：∵在Rt△ABC中，∠ACB=90°，sinB=
，
∴设b=5x，则c=13x，
则a=
=12x，
∴tanA=
=
=
．
故选C．
解：∵在Rt△ABC中，∠ACB=90°，sinB=| 5 |
| 13 |
∴设b=5x，则c=13x，
则a=
| c2-b2 |
∴tanA=
| a |
| b |
| 12x |
| 5x |
| 12 |
| 5 |
故选C．
点评：本题考查了互余两角三角函数的关系，利用锐角三角函数的定义，通过设参数的方法求三角函数值．
练习册系列答案
举一反三同步巧讲精练系列答案
相关题目
化简
-
的结果是（ ）
| x2 |
| x-y |
| y2 |
| x-y |
| A、-x-y | B、y-x |
| C、x-y | D、x+y |
下列说法不正确的是（ ）
| A、等腰梯形的对角线相等 |
| B、矩形的对角线互相垂直 |
| C、对角线互相垂直平分的四边形是菱形 |
| D、一组对边平行且相等的四边形是平行四边形 |
点P（m+3，m+1）在x轴上，则P点坐标为（ ）
| A、（0，-2） |
| B、（0，-4） |
| C、（4，0） |
| D、（2，0） |
如图所示的图形中：其中是轴对称图形的共有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
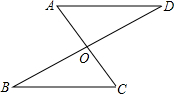如图，已知AC与BD交于点O，AD∥BC，且AD=BC，求证：BO=DO．
如图，两块相同的直角三角板拼成一个图形．