题目内容
将等边△ABC绕自身的内心O,顺时针至少旋转n°,就能与自身重合,则n等于( )
| A、60 | B、120 |
| C、180 | D、360 |
考点:旋转对称图形
专题:
分析:等边三角形的外心到三个顶点的距离相等,相邻顶点与外心连线的夹角相等,计算旋转角即可.
解答:解:因为等边三角形的外心到三个顶点的距离相等,相邻顶点与外心连线的夹角相等,
所以,360°÷3=120°,即每次至少旋转120°.
故选:B.
所以,360°÷3=120°,即每次至少旋转120°.
故选:B.
点评:本题考查旋转对称图形的概念:把一个图形绕着一个定点旋转一个角度后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转的角度叫做旋转角.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
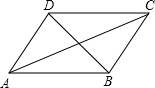 如图,四边形ABCD是平行四边形,下列说法不正确的是( )
如图,四边形ABCD是平行四边形,下列说法不正确的是( )| A、当AC=BD时,四边形ABCD是矩形 |
| B、当∠DAB=90°时,四边形ABCD是正方形 |
| C、当AC⊥BD时,四边形ABCD是菱形 |
| D、当AB=BC时,四边形ABCD是菱形 |
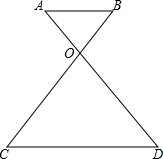 如图,AD与BC交与点O,且AB∥CD.
如图,AD与BC交与点O,且AB∥CD.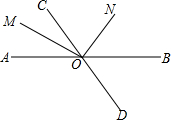 如图,OM平分∠AOC,OM⊥ON,∠BOD=70°,求∠CON.
如图,OM平分∠AOC,OM⊥ON,∠BOD=70°,求∠CON.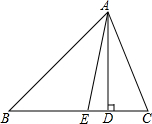 如果,在△ABC中,AD是高,AE是∠BAC的平分线,∠BAC=54°,∠C=70°.求∠EAD的度数.
如果,在△ABC中,AD是高,AE是∠BAC的平分线,∠BAC=54°,∠C=70°.求∠EAD的度数.