题目内容
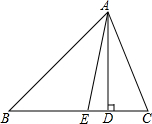 如果,在△ABC中,AD是高,AE是∠BAC的平分线,∠BAC=54°,∠C=70°.求∠EAD的度数.
如果,在△ABC中,AD是高,AE是∠BAC的平分线,∠BAC=54°,∠C=70°.求∠EAD的度数.考点:三角形内角和定理,三角形的外角性质
专题:
分析:先根据三角形内角和定理求出∠DAC,根据角平分线定义求出∠EAC,代入∠DAE=∠EAC-∠DAC求出即可.
解答:解:∵AD是搞,
∴∠ADC=90°,
∵∠C=70°,
∴∠DAC=20°,
∵AE是∠BAC的平分线,∠BAC=54°,
∴∠EAC=
∠BAC=27°,
∴∠EAD=∠EAC-∠DAC=27°-20°=7°.
∴∠ADC=90°,
∵∠C=70°,
∴∠DAC=20°,
∵AE是∠BAC的平分线,∠BAC=54°,
∴∠EAC=
| 1 |
| 2 |
∴∠EAD=∠EAC-∠DAC=27°-20°=7°.
点评:本题考查了三角形内角和定理,垂直定义,角平分线定义的应用,解此题的关键是求出∠DAC和∠EAC的度数,难度适中.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
 如图,已知AD∥BC,AP平分∠DAB,BP平分∠ABC,点P恰好在CD上,王玲同学根据给定的条件写出了四个结论:①AP⊥BP;②点P到AD,BC的距离相等;③PD=PC;④AD+BC=AB,其中结论正确的个数有( )
如图,已知AD∥BC,AP平分∠DAB,BP平分∠ABC,点P恰好在CD上,王玲同学根据给定的条件写出了四个结论:①AP⊥BP;②点P到AD,BC的距离相等;③PD=PC;④AD+BC=AB,其中结论正确的个数有( )| A、1个 | B、2个 | C、3个 | D、4个 |
将等边△ABC绕自身的内心O,顺时针至少旋转n°,就能与自身重合,则n等于( )
| A、60 | B、120 |
| C、180 | D、360 |
 如图,已知圆O的直径为6,CD为圆O的直径,且CD⊥AB,∠D=15°.则OE的长为( )
如图,已知圆O的直径为6,CD为圆O的直径,且CD⊥AB,∠D=15°.则OE的长为( )| A、3 | ||||
B、3
| ||||
C、
| ||||
D、
|
已知ab≠0,则
+
的值有( )
| |a| |
| a |
| |b| |
| b |
| A、唯一确定的值 |
| B、两种不同的值 |
| C、三种不同的值 |
| D、四种不同的值 |
 如图,DE∥BC,DF∥AB,∠1=70°,求∠D、∠2和∠3的度数.
如图,DE∥BC,DF∥AB,∠1=70°,求∠D、∠2和∠3的度数. 如图,已知∠1=∠2=∠3=∠4=∠5,延长AB、GF交于点M,试探索∠M与∠3的关系,说明理由.
如图,已知∠1=∠2=∠3=∠4=∠5,延长AB、GF交于点M,试探索∠M与∠3的关系,说明理由.