题目内容
16．如果抛物线y=2x2+mx+n的顶点坐标为（1，3），那么m+n的值等于1．分析 根据抛物线y=2x2+mx+n的顶点坐标为（1，3），可知$-\frac{m}{2×2}=1，\frac{4×2×n-{m}^{2}}{4×2}=3$，从而可以得到m、n的值，进而可以得到m+n的值．
解答 解：∵抛物线y=2x2+mx+n的顶点坐标为（1，3），
∴$-\frac{m}{2×2}=1，\frac{4×2×n-{m}^{2}}{4×2}=3$，
解得m=-4，n=5，
∴m+n=-4+5=1．
故答案为：1．
点评 本题考查二次函数的性质，解题的关键是明确二次函数的顶点坐标公式．
练习册系列答案
相关题目
6．-3的相反数是（ ）
| A． | $\frac{1}{3}$ | B． | -$\frac{1}{3}$ | C． | -3 | D． | 3 |
5．
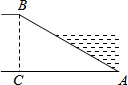如图，河坝横断面迎水坡AB的坡比是1：$\sqrt{3}$（坡比是坡面的铅直高度BC与水平宽度AC之比），坝高BC=3m，则坡面AB的长度是（ ）
如图，河坝横断面迎水坡AB的坡比是1：$\sqrt{3}$（坡比是坡面的铅直高度BC与水平宽度AC之比），坝高BC=3m，则坡面AB的长度是（ ）| A． | 9m | B． | 6m | C． | 6$\sqrt{3}$m | D． | 3$\sqrt{3}$m |