题目内容
18.当a≠-$\frac{1}{3}$时,关于x的方程(3a+1)x2+5ax+4=0是一元二次方程.分析 根据一元二次方程的定义得到3a+1≠0,由此求得a的取值范围.
解答 解:∵关于x的方程(3a+1)x2+5ax+4=0是一元二次方程,
∴3a+1≠0,
解得a≠-$\frac{1}{3}$.
故答案是:≠-$\frac{1}{3}$.
点评 本题利用了一元二次方程的概念.只有一个未知数且未知数最高次数为2的整式方程叫做一元二次方程,一般形式是ax2+bx+c=0(且a≠0).特别要注意a≠0的条件.这是在做题过程中容易忽视的知识点.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
7.计算结果不可能m8的是( )
| A. | m4•m4 | B. | (m4)2 | C. | (m2)4 | D. | m4+m4 |
8.无论x取何值,总是有意义的分式是( )
| A. | $\frac{x}{2x+1}$ | B. | $\frac{2x}{{x}^{2}+1}$ | C. | $\frac{3x}{{x}^{3}+1}$ | D. | $\frac{x+1}{{x}^{2}}$ |
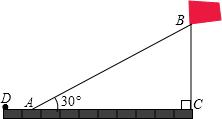 如图,小明利用升旗用的绳子测量学校旗杆BC的高度,当绳子从旗杆端垂下,地上部分还有8米,若把绳子往外拉直,绳子末端接触地面A点并与地面形成30°角,求旗杆BC的高度.
如图,小明利用升旗用的绳子测量学校旗杆BC的高度,当绳子从旗杆端垂下,地上部分还有8米,若把绳子往外拉直,绳子末端接触地面A点并与地面形成30°角,求旗杆BC的高度.
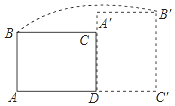 如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕点D顺时针旋转90°得到矩形A′B′C′D′,则点B经过的路径与BA,AC′,C′B′所围成封闭图形的面积是多少?(结果保留π).
如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕点D顺时针旋转90°得到矩形A′B′C′D′,则点B经过的路径与BA,AC′,C′B′所围成封闭图形的面积是多少?(结果保留π).