题目内容
13.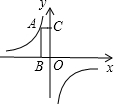 A是双曲线y=-$\frac{5}{x}$上一点,过点A向x轴作垂线,垂足为B,向y轴作垂线,垂足为C,则四边形OBAC的面积为( )
A是双曲线y=-$\frac{5}{x}$上一点,过点A向x轴作垂线,垂足为B,向y轴作垂线,垂足为C,则四边形OBAC的面积为( )| A. | 6 | B. | 5 | C. | 10 | D. | -5 |
分析 由“点A在双曲线y=-$\frac{5}{x}$上,且AC⊥y轴,AB⊥x轴”结合反比例函数系数k的几何意义,即可得出四边形OBAC的面积.
解答 解:∵点A在双曲线y=-$\frac{5}{x}$上,且AC⊥y轴,AB⊥x轴,
∴S矩形OBAC=|k|=5.
故选B.
点评 本题考查了反比例函数系数k的几何意义,熟练掌握反比例函数系数k的几何意义是解题的关键.

练习册系列答案
相关题目
8.无论x取何值,总是有意义的分式是( )
| A. | $\frac{x}{2x+1}$ | B. | $\frac{2x}{{x}^{2}+1}$ | C. | $\frac{3x}{{x}^{3}+1}$ | D. | $\frac{x+1}{{x}^{2}}$ |
2.下列各式分解因式正确的是( )
| A. | x3-x=x(x2-1) | B. | x2-x+0.25=(x-0.5)2 | ||
| C. | (a+4)(a-4)=a2-16 | D. | x2+y2=(x+y)(x-y) |
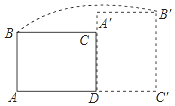 如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕点D顺时针旋转90°得到矩形A′B′C′D′,则点B经过的路径与BA,AC′,C′B′所围成封闭图形的面积是多少?(结果保留π).
如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕点D顺时针旋转90°得到矩形A′B′C′D′,则点B经过的路径与BA,AC′,C′B′所围成封闭图形的面积是多少?(结果保留π). 已知:如图,A、C、F、D在同一直线上,AF=DC,AB∥DE,AB=DE,求证:
已知:如图,A、C、F、D在同一直线上,AF=DC,AB∥DE,AB=DE,求证: